Wiskundemeisjes
In de cryptografie willen Alice en Bob elkaar aldoor geheime boodschappen sturen. En dit is blijkbaar hoe het begon:

Lees bij Abstruse Goose hoe het verder ging.
Deze column verscheen in de Volkskrant op 25 april 2009.
Ik kom uit een familie van hypochonders. Onze huisartsen zijn inmiddels gewend aan nachtelijke telefoontjes omdat we ineens denken dat we acute nekkramp of iets anders vreselijks hebben. Als ik een artikel lees over een zeldzame ongeneeslijke ziekte, dan denk ik onmiddellijk dat ik die ook heb. Ik herken namelijk de symptomen: ik ben vaak moe en bovendien heb ik wel eens hoofdpijn. Op zo’n moment zegt mijn vriend meestal dat ik de krant maar eens moet wegleggen en lekker met hem in de zon op een terrasje gaan zitten.

Heel soms laat ik me toch op iets testen en terwijl ik wacht op de uitslag denk ik dan na over wiskunde. Stel bijvoorbeeld dat één op de tienduizend mensen een bepaalde ziekte heeft en dat er een test voor deze ziekte bestaat die 99% betrouwbaar is. Dit betekent dat de test bij 99% van de personen die aan deze ziekte lijden een positieve uitslag geeft. Andersom geeft de test bij 99% van de personen die niet lijden aan deze ziekte een negatieve uitslag. Stel dat ik me laat testen met deze test (die 99% procent betrouwbaarheid klinkt me immers goed in de oren) en dat de uitslag positief is. Hoe groot is dan de kans dat ik deze ziekte heb?
Denk maar even rustig na. Wat lijkt aannemelijk? Ongeveer 1%, 50% of 99%? Leg anders de krant even weg en ga er over nadenken in de zon op een terrasje.

De artsen proberen mijn testuitslag te begrijpen...
Ik neem trouwens aan dat mensen die zich laten testen geen hoger risico hebben op de ziekte, ze laten zich zonder aanleiding testen. Het enigszins verbazingwekkende juiste antwoord is dan dat de kans dat ik ziek ben minder is dan 1%. Reken maar mee: stel voor het gemak dat in totaal één miljoen mensen zich laat testen. Dezelfde berekening geldt voor een willekeurig aantal geteste mensen, maar met één miljoen rekent het wat makkelijker. We weten dat één op de tienduizend mensen de ziekte heeft: dat zijn in een groep van één miljoen dus honderd zieken. Van die honderd geeft de test in 99 gevallen als uitslag `positief’, één iemand krijgt de foutieve uitslag `negatief’. Daarnaast zijn er 999.900 gezonde mensen die zich laten testen. Van deze groep krijgt 1% onterecht de melding `positief’, dat zijn 9.999 mensen. De andere 998.901 gezonde mensen krijgen keurig de negatieve uitslag.
In totaal krijgen dus 10.098 mensen een positieve testuitslag, terwijl maar 99 daarvan de ziekte echt hebben. Als ik een positieve testuitslag krijgt is de kans dat ik deze ziekte heb dus 99/10.098 en dat komt neer op 0.98%. De test met 99% betrouwbaarheid blijkt toch niet zo heel betrouwbaar – ook al krijgt 99% van de mensen die de test doen de juiste uitslag.
In de praktijk worden testen gebruikt die een hogere betrouwbaarheid hebben – dus een valse positiefmelding is erg zeldzaam. Een valse negatiefmelding is ook zeldzaam, maar een echte hypochonder trekt zich daar natuurlijk niets van aan. Laatst zag ik trouwens ineens een raar vlekje op mijn arm, misschien moet ik daar toch ook maar eens naar laten kijken.
Deze boekrecensie verscheen vorige week in Delta, weekblad van de Technische Universiteit Delft.
Van het slijpen van diamanten tot verkiezingsparadoxen en van lottokansen tot de stelling van Pythagoras. Honderd wiskundige onderwerpen in een kleine driehonderd pagina’s. Weinig essentieel, maar wel onderhoudend, stelt Ionica Smeets.
Jaren geleden hoorde ik een geweldige anekdote over een Russische professor die werd overvallen door een bende rovers. De rovers dachten dat hij een of andere spion was. Toen de arme man stamelde dat hij een wiskundige was, zei de rovershoofdman: “Wiskunde? Goed! Geef me dan maar eens een schatting voor de fout die je maakt bij het afkappen van de Maclaurin-reeks bij de n-de term!” Nerveus deed de professor wat hem gevraagd werd. “Inderdaad, je bent een wiskundige”, zei de hoofdman na afloop: “Je bent vrij om te gaan.” De wiskundige heeft zich jarenlang afgevraagd waarom deze rover wist wat een Maclaurin-reeks was.
Ik vond het een prachtig verhaal, maar ik was vergeten wie de wiskundige was en dat van die reeks had ik ook niet zo precies onthouden. Toen iemand me vertelde dat deze anekdote in '100 Essential Things You Didn't Know You Didn't Know' stond, was ik ontzettend benieuwd naar de rest van de verhalen. De wiskundige uit de anekdote bleek trouwens een natuurkundige te zijn: het was Igor Tamm die in 1958 een Nobelprijs voor natuurkunde kreeg. De anekdote is hoofdstuk 44 onder het motto 'met analyse leef je langer.'

Elk hoofdstuk beslaat twee of drie pagina's en de onderwerpen lopen wijd uiteen: van het slijpen van diamanten tot verkiezingsparadoxen en van lottokansen tot de stelling van Pythagoras. Een groot deel van de voorbeelden is helaas vrij bekend en weinig dingen in het boek zijn echt essentieel. Na het lezen bedacht ik dat een betere titel voor dit boek zou zijn: '40 things you probably read somewhere else, 30 things you do not really care about and 30 things that are very cool'.
Het niveau van de stukken verschilt flink, daardoor is niet helemaal duidelijk wat de doelgroep is van het boek. Is '100 Essential Things' bedoeld voor leken die helemaal niets van wiskunde weten? Daarvoor lijken sommige dingen net iets te lastig, met formules en wiskundige notatie. Aan de andere kant, als het boek niet bedoeld is voor leken, dan is het erg jammer dat veel voorbeelden uit eerstejaarscolleges voorbij komen.
Toch is '100 Essential Things' absoluut niet slecht in zijn genre. Barrow schreef al een hele stapel populair-wetenschappelijke boeken en hij vertelt helder en geestig. Elk hoofdstuk begint hij met een goed gekozen citaat. Bij een stuk over de metrokaart van Londen citeert hij bijvoorbeeld David Hockney: 'Art has to move you and design does not, unless it's a good design for a bus.'
Bovendien staat er tussen de honderd verhalen een aantal dat zo fantastisch is, dat alleen die al de aankoop van het boek rechtvaardigen. De diversiteit van de hoofdstukken is hier een voordeel: leken vinden waarschijnlijk heel andere dingen interessant dan beroepsbèta's. Mijn favorieten waren de anekdotes. Bijvoorbeeld over een bizarre voetbalwedstrijd tussen Grenada en Barbados. In het toernooi werd een nieuwe regel gebruikt: als een team in de verlenging scoorde, dan stopte het spel onmiddellijk en telde die gouden goal als twee doelpunten. Barbados moest met twee punten verschil winnen om door te gaan naar de volgende ronde.
Barbados stond met 2-0 voor toen zeven minuten voor het einde Grenada 2-1 scoorde. Een speler van Barbados bedacht dat het lastig was om in die laatste minuten nog een goal te maken en schoot rustig in eigen doel. Nu was het 2-2 en kon Barbados in de verlenging winnen door een gouden goal te scoren. Tenzij...Grenada nog in de speeltijd een doelpunt maakte, onverschillig of dat in hun eigen doel of dat van de tegenstander was. Zowel met 3-2 als 2-3 zou Grenada immers winnen. De spelers van Barbados besloten daarop het doel van Grenada te verdedigen. Niet essentieel, maar wel leuk om te weten!
John D. Barrow - `100 Essential Things You Didn't Know You Didn't Know ', The Bodley Head London, pp 284, 14 euro.
De BBC zendt al een paar jaar het programma More or less uit op de radio. Van de website:
We like to think that More or Less has no particular subject.
Rather it touches on every subject, with the same calm authority.
We all use numbers in so many ways to argue about, understand, help make sense of the world around us.
More or Less hopes to make that task easier, more entertaining, more surprising.
Over wiskunde in de echte wereld dus, voor een breed publiek!

Presentator Tim Harford
Op 17 april is de nieuwe serie begonnen. De meest recente aflevering is online terug te luisteren, net als de oudere afleveringen in het archief.
Op de website staan een paar filmpjes, waarin programma-gasten uitleggen wat zij met getallen hebben. Marcus du Sautoy vertelt bijvoorbeeld waarom 17 zijn favoriete getal is. Leuk!
Op het nippertje, want aanmelden kan tot morgen: vrijdag aanstaande kun je op de UvA naar Leve de wiskunde!. Dat is een congres voor wiskundedocenten, geïnteresseerde 6-vwo-scholieren en andere belangstellenden.

De onderwerpen die aan de orde komen zijn:
De wiskunde achter knopen (Jasper Stokman)
Kansloos: van Willem Ruis tot Lucia de B. (Peter Grünwald)
De kredietcrisis vanuit wiskundig perspectief (Robin de Vilder)
De Wiskunde Club (Doortje de Wiljes en Kyndylan Nienhuis)
`Sex and the City': eenvoudige modellen voor complexe netwerken (Peter Sloot)
Kortom: een boel leuks! Kijk op de website voor programma en locatie, voor de samenvattingen van de voordrachten en voor het aanmeldformulier.
Zoals onlangs beloofd: iets meer over Edsger W. Dijkstra. Deze column verscheen eerder in Technisch Weekblad, vakblad voor hogeropgeleide technici en bèta's.
Vijftig jaar geleden publiceerde Edsger Dijkstra zijn kortstepadalgoritme. Daarom een kleine ode aan de in 2002 overleden Dijkstra, iemand waar we als Nederlanders best wat trotser op mogen zijn. Dijkstra was een van de eerste programmeurs van Nederland. Toen hij in 1957 trouwde, werd het beroep computerprogrammeur door de burgerlijke stand nog niet erkend en uiteindelijk gaf hij maar `theoretische natuurkundige’ op.
Zijn beroemdste resultaat is het kortstepadalgoritme, dat de kortste verbinding vindt tussen twee knopen in een graaf (een verzameling punten waarvan sommigen verbonden zijn). Denk bijvoorbeeld aan het vinden van de kortste route tussen twee steden. Het slimme van Dijkstra’s algoritme is dat het niet alle mogelijke routes met elkaar vergelijkt, maar dat het stap voor stap de kortst mogelijke afstanden tot elk punt opbouwt. In de eerste stap kijk je naar alle punten die vanaf het beginpunt te bereiken zijn en markeer je al die punten met de afstand tot het beginpunt. Daarna kijk je steeds vanaf het punt dat op dat moment de kortste afstand heeft tot het beginpunt naar alle punten die je vanaf daar kunt bereiken. Als je een buurpunt via een nieuwe verbinding op een snellere manier kunt bereiken, schrijf je de nieuwe, kortere afstand tot het beginpunt bij zo’n punt. Zo ga je steeds een stukje verder tot je alle punten hebt gehad en je de kortste route tot het eindpunt hebt gevonden.
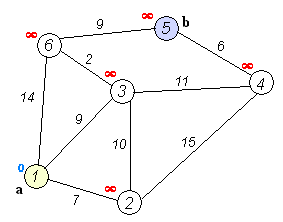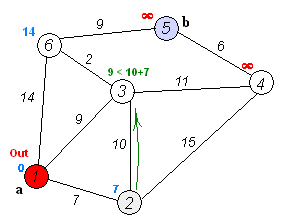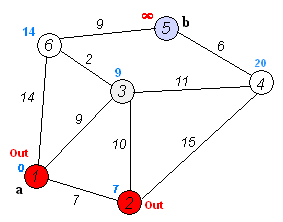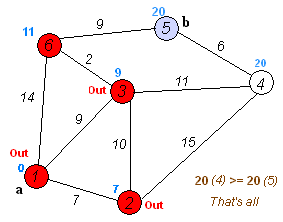
Als je het algoritme even op een servetje probeert, dan is is het zo eenvoudig dat je je afvraagt waarom je het niet zelf hebt bedacht. Dijkstra vond het zelf ook een beetje gek dat zijn naam en faam voor een groot deel gebaseerd waren op een algoritme dat hij bedacht als demonstratie voor een computer. Hij bedacht het kortstepadalgoritme zonder pen of papier op een zonnig terras terwijl hij met zijn vrouw een kopje koffie dronk.

Dijkstra verzon nog veel meer dan dit algoritme en hij had ook sterke visie op wat informatica zou moeten zijn. Honderden brieven, essays en andere handgeschreven teksten van Dijkstra staan op internet (E. W. Dijkstra Archive). Elke tekst heeft de code EWD (van Edsger W. Dijkstra) en een nummer, EWD1213 is bijvoorbeeld een inleiding bij een cursus analyse. De manier waarop hij zijn studenten daarin toespreekt, is prachtig:
It is not my purpose to "transfer knowledge" to you that, subsequently, you can forget again. My purpose is no less than to effectuate in each of you a noticeable, irreversable change. [...] I mean, if 10 years from now, when you are doing something quick and dirty, you suddenly visualize that I am looking over your shoulders and say to yourself “Dijkstra would not have liked this.”, well, that would be enough immortality for me.
Zou het hem ooit gelukt zijn dit te bereiken bij zijn studenten? De komende weken zal ik in elk geval schuldbewust aan Dijkstra denken als ik een lompe brute-force-oplossing gebruik.
Tot mijn grote vreugde las ik zojuist in de NewScientist een nieuwsbericht over breuken. Simon N. Jacob en Andreas Nieder van de Universiteit Tübingen scanden de hersenen van volwassenen die allerlei breuken te zien kregen. En blijkbaar worden breuken door onze hersenen direct geïnterpreteerd, we zien ze dus niet als twee losse gehele getallen die je door elkaar moet delen. Bij het zien van dezelfde breuk in verschillende notaties wordt steeds hetzelfde deel van de hersenen geactiveerd. Het artikel waarin de resultaten gepresenteerd worden heet Notation-Independent Representation of Fractions in the Human Parietal Cortex en het verscheen deze maand in The Journal of Neuroscience.
Ik wacht nu op onderzoekers die kijken hoe kettingbreuken in de hersenen worden ontvangen.
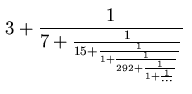
Ik vermoed dat bovenstaand voorbeeld bij mij ongeveer dezelfde delen van mijn hersenen activeert als giraffen, Jarvis Cocker, palmbomen, pi en chocoladerozijnen.
Brecht mailde ons een tijdje terug: "Mochten jullie binnenkort iets over een tangram op jullie blog plaatsen, dan lijkt dit me wel leuke randinformatie."

Wij vinden het leuk genoeg om een speciale post aan deze Tangram kasten te wijden! Past mooi bij meubels die we hier eerder plaatsten.
Vandaag start de internetboekenveiling van het Wereldwiskunde Fonds, een van de werkgroepen van de NVvW (de Nederlandse Vereniging van Wiskundeleraren). Het doel van het Wereldwiskunde Fonds (WwF) is ondersteuning van het wiskundeonderwijs in derde-wereldlanden door middel van financiële bijdragen aan projecten. Ook wil het WwF aan wiskundedocenten 'hier' laten zien dat er 'daar' ook collega's zijn die zich met soortgelijke vragen en problemen bezighouden als zij zelf, maar ook met heel andere.

Een van de manier waarop het WwF fondsen werft is deze internetboekenveiling, waar tweedehands wiskundeboeken bij opbod verkocht worden. Misschien zit er wel iets van jouw gading bij!
De veiling opent vandaag en sluit op 31 mei 2009 om 23.59 uur.
Deze column verscheen in de Volkskrant op 11 april 2009.
Veel wiskundigen die ik ken houden van spelletjes. Ik speel dan ook regelmatig een avondje Kolonisten van Catan of Carcassonne met mijn collega’s. En als je een spel speelt, wil je natuurlijk het liefst winnen. Wiskundigen hebben daarom een heleboel spellen bestudeerd om een optimale strategie te vinden.
Bij veel spelletjes is niet van tevoren met zekerheid te zeggen wie er zal winnen, zelfs niet als je aanneemt dat alle spelers optimaal slim spelen. In poker bijvoorbeeld zit altijd een kanselement. Je kunt uitrekenen dat de kans op een paartje azen stukken groter is dan de kans op een royal flush, maar de garantie dat een van de spelers met een bepaalde strategie zeker zal winnen is er niet. Hetzelfde geldt voor Kolonisten van Catan en Carcassonne.
Andere spellen, bijvoorbeeld schaken en boter-kaas-en-eieren, hebben geen kanselement. Je bent in die spellen niet afhankelijk van willekeurig getrokken kaarten of van wat je gooit met een dobbelsteen. Voor spellen zonder kanselement bestaat er soms een winnende strategie voor een van de spelers. Dat wil zeggen dat je altijd wint als je deze strategie volgt - wat de andere speler ook doet.
Een voorbeeld van een spelletje met een winnende strategie is het volgende luciferspel voor twee spelers. Er liggen 21 lucifers op tafel. Iedere speler neemt als hij aan de beurt is één, twee of drie lucifers weg. Wie de laatste lucifer moet pakken, verliest. Wat is het beste om te doen? En maakt het uit wie er begint?

Stel dat u het spel tegen mij speelt. Uit beleefdheid laat ik u beginnen, en u pakt twee lucifers weg. Dan neem ik er ook twee. Vervolgens pakt u er eentje, dan neem ik er drie. Zo gaan we een paar beurten door, en uiteindelijk ligt er na mijn vijfde beurt nog maar één lucifer op tafel, zodat u verliest. Hoe kan dat?
Het feit dat ik u laat beginnen zou al een alarmbel moeten laten rinkelen: er is in dit spel een winnende strategie voor de tweede speler. Wat ik als tweede speler doe is namelijk het volgende. Als u één lucifer neemt, neem ik er drie. Als u er twee neemt, pak ik er ook twee. En als u er drie neemt, neem ik er eentje. In totaal verdwijnen er dus elke keer wanneer we allebei aan de beurt geweest zijn vier lucifers. Na vijf beurten ieder zijn er dus twintig lucifers weg, en is er nog één over!
Voor schaken is zo’n winnende strategie nog niet gevonden, dat is vreselijk gecompliceerd. Spellen zonder kanselement hoeven ook helemaal geen winnende strategie te hebben. Boter-kaas-en-eieren bijvoorbeeld eindigt altijd in remise als allebei de spelers optimaal slim spelen.
Natuurlijk maakt het bekend zijn van een winnende strategie een spel meteen stukken minder leuk: je weet van tevoren al precies wat er zal gaan gebeuren en wie er gaat winnen, en dan is de lol er wel af. Maar als uw familieleden de krant vandaag nog niet gelezen hebben, maakt u een goede kans met het luciferspel!
 Internetbureau Rotterdam
Internetbureau Rotterdam 
