Wiskundemeisjes

Beste loterij-verliezer,

Deze week was u ineens toch een beetje een winnaar toen de rechtbank besloot dat de Staatsloterij haar deelnemers tot 2008 misleidde. Met een beetje geluk krijgt u zelfs uw geld terug. Het was natuurlijk ook enorm oneerlijk wat die loterij deed. Ze verkochten drie miljoen loten, maar trokken de prijzen uit een verzameling van eenentwintig miljoen loten. Als u dát had geweten, dan had u natuurlijk nooit een lot gekocht!

Hoewel, iets zegt me dat u waarschijnlijk niet zo goed bent in kansen uitrekenen. Laten we eens kijken naar de twintig prijzen van 100.000 euro die de Staatsloterij maandelijks beloofde. Als ze die prijzen keurig uit de verkochte loten trokken, dan was uw kans om te winnen één op honderdvijftigduizend. Als u maandelijks meespeelt, dan moet u daarmee naar verwachting een slordige twaalfduizend jaar wachten op zo’n prijs. En dan was dit nog in het gunstige geval waarbij de Staatsloterij u níet misleidde. U mag natuurlijk hopen dat u net geluk heeft binnen de schamele tachtig jaar dat u leeft, maar als ik u was zou ik er niet op rekenen.

Ter vergelijking: als u twintig jaar lang vijftien euro op een spaarrekening stort (in plaats van een lot te kopen), dan heeft u bij een gemiddelde rente van drie procent aan het einde bijna vijfduizend euro. Een loterij zou in dit geval zeggen dat ze 136 procent van uw inzet uitkeren.

De Staatsloterij keert daarentegen iets meer dan zestig procent van de inleg uit. De rest van het geld verdwijnt in de staatskas. Iemand grapte ooit dat loterijen een belasting zijn voor mensen die slecht zijn in wiskunde. Dat lijkt in dit geval extra toepasselijk, want de Staatsloterij spekt de staatskas dubbel. Van de uitgekeerde inleg betaalt de loterij namelijk ook nog kansspelbelasting. Kortom, door mee te doen aan de Staatsloterij betaalt u mooi mee aan de studie van mensen die straks begrijpen waarom het beter is om niet mee te doen aan loterijen.

Dankzij noest speurwerk van Twitter weet ik nu dat de grap over loterij als belasting al in 1662 gemaakt werd door Sir William Petty. Hij schreef:

A Lottery therefore is properly a Tax upon unfortunate self-conceited fools; men that have good opinion of their own luckiness, or that have believed some Fortuneteller or Astrologer, who had promised them great success about the time and place of the Lottery, lying Southwest perhaps from the place where the destiny was read.

Meer in zijn verzamelde werken.

Let ook eens op de winkans waarover de Staatsloterij graag roept dat het de grootste van Nederland is. Die kans klinkt best indrukwekkend: bij elke trekking valt op maar liefst 53,8% van de verkochte loten een prijs. Je wint dus meer de helft van de keren dat je meespeelt! Er zit alleen een klein addertje onder het gras: veel van die prijzen zijn kleiner dan de kosten van een lot. De kans dat je een prijs wint die hoger is dan je eigen inleg is 18,5 procent. Eerlijk is eerlijk: bij andere loterijen is het inderdaad nóg beroerder.

Het valt me op dat het proces tegen de Staatsloterij zelf ook wel iets van een loterij heeft. Op de website waar gedupeerden zoals u zich kunnen aanmelden staat: “Deelname aan het proces tegen de Staatsloterij kost u éénmalig € 35 inschrijfgeld voor één meegespeeld lot, plus € 10,00 voor elk volgend lot, ongeacht de periode.” Jammer dat er niet bijstaat wat de winkans hier is. Al durft u waarschijnlijk wel een gokje te wagen.

Succes!

Ionica

Deze column verscheen afgelopen weekend in de Volkskrant.

Deze column verscheen afgelopen weekend in de Volkskrant.

Beste Malcolm Gladwell,

Ik weet niet hoeveel uren ik de afgelopen jaren moest luisteren naar mensen die zeurden over de tienduizend-uren-regel. Want dankzij uw boek Uitblinkers weet iedereen dat je overal goed in kunt worden, als je maar tienduizend uur oefent. Of je nu droomt van een baan als profvoetballer of topwiskundige, je moet domweg heel veel trainen. Eindelijk een duidelijk antwoord op de eeuwenoude vraag over talent: Is dat aangeboren, of vooral een kwestie van hard werken?

U ontdekte de tienduizend-uren-regel in een wetenschappelijke studie. Daaruit bleek dat de beste violisten en pianisten meer dan tienduizend uur hadden geoefend voordat ze twintig waren (spelen voor de lol telde trouwens niet mee, het was blijkbaar niet de bedoeling dat de kinderen er plezier in hadden). Dát maakte dat ze zo goed waren. Aangeboren talent speelde geen enkele rol, hooguit het talent om flink te willen oefenen. Iedereen die tienduizend uur actief aan een vak besteed, zal excellent worden. En niemand bereikt de top zonder die tienduizend uur training. Met uw boek verspreidde u deze ideeën onder het grote publiek. U legt uit dat The Beatles en Bill Gates flink wat uren maakten voordat ze succes boekten. Terloops laat u subtiel vallen dat ú de tienduizend uur als journalist ruimschoots gehaald heeft.

Minder bekend is dat Malcolm Gladwell ook tienduizend uur oefende op een nonchalante pose.

Die tienduizend uur is een heerlijk duidelijke grens. Hij maakt ook gelijk duidelijk waarom het zo moeilijk is om de top te bereiken. Met vier uur per week voetballen, duurt het bijna vijftig jaar voor je genoeg getraind hebt (al vermoed ik dat je dan te oud zult zijn om nog echt door te breken als international). Het is ook verleidelijk om zelf even te controleren waaraan je tienduizend uur hebt besteed. Zelf kom ik met wiskunde na vijf jaar studie en vier jaar promotie-onderzoek aardig in de buurt. Toch heb ik nog steeds geen beroemd resultaat bewezen, laat staan dat ik een Fieldsmedaille heb gewonnen.

Aan de ene kant is het idee van die tienduizend uur erg opbeurend. Je kunt over tien jaar de volgende Janine Jansen zijn; je hoeft daarvoor alleen maar even twintig uur per week te oefenen. Aan de andere kant is het idee ook wat deprimerend: het is je eigen schuld als je nergens excellent in bent.

Deze maand verscheen er echter een studie die laat zien dat het allemaal helemaal niet zo simpel ligt. Onderzoekers keken bijvoorbeeld naar schakers. Ze ontdekten dat sommige spelers al meester worden na een schamele 2.500 uur oefenen. Maar er zijn ook zielenpoten die meer dan 20.000 uur trainen en desondanks middelmatig blijven. Niet iedereen kan dus alles leren door er genoeg tijd aan te besteden. De nieuwe studie schat dat bij schakers oefenen slechts vierendertig procent van het verschil in prestaties verklaart. Voor muzikanten is dat percentage nog kleiner. Kortom: tienduizend uur oefenen is geen garantie voor succes en sommige geluksvogels hebben veel minder tijd nodig om de top te bereiken. Daar gaat uw gulden regel?

Maakt u nu een nieuw boek? Of bent u zelf nog steeds verbeten aan het oefenen om profvoetballer te worden?

Zet hem op!

Ionica

Deze column verscheen afgelopen weekend in de Volkskrant.

Beste scholieren van Nederland,

Wat goed dat jullie een krant lezen! En dat met jullie beperkte aandachtsspanne. Knap man. Laat ik snel doorgaan voor jullie weer op YouTube naar filmpjes van Justin Bieber kijken (of doen jullie dat gewoon tijdens het lezen?). Ik heb namelijk een tip voor jullie eindexamens.

Deze week kregen jullie weer eens kritiek op jullie zesjesmentaliteit: de afgelopen jaren schommelde het gemiddelde eindexamencijfer op HAVO en VWO iets boven de zes. Maar wacht eens, worden die eindexamens niet genormeerd zodat het gemiddelde daar ongeveer ligt? Ik probeerde uit te zoeken hoe de eindcijfers uiteindelijk bepaald worden en belandde in een oerwoud van documenten vol vage taal. Als jullie zulke zinnen gebruikten in je eindexamen Nederlands, dan konden jullie dat zesje mooi op je buik schrijven. De korte samenvatting dan maar.

Eén van de aannames bij de normering is dat vaardigheden van scholieren in opeenvolgende jaren zelden grote sprongen maken. Dus zullen de gemiddelde cijfers ná normering elk jaar ongeveer hetzelfde zijn. Verder is de normering zo opgesteld dat wie niets goed heeft altijd een één krijgt, en wie alles goed heeft een tien. Om nu te zorgen dat de cijfers er verder een beetje netjes uitzien, moet het aantal onvoldoendes na normering tussen de vijftien en vijfendertig procent liggen.

Wetenschappelijk onderbouwd trouwens dat percentage onvoldoendes: "Dat blijkt redelijke gemiddelde slaagkans te bieden en een redelijk 'voordeel van de twijfel'." (Klik voor meer ellende)

Stel nu eens dat jullie allemaal met een negenmentaliteit gaan leren en bij het eindexamen stuk voor stuk een voldoende halen. Dan zal de normering zo aangepast worden dat de minst goede leerlingen alsnog een onvoldoende krijgen. Zo komen jullie gemiddeld toch weer uit rond de zes en kunnen alle vijftigers lekker klagen dat de jeugd van tegenwoordig zo dom en lui is.

Ach, het was jullie vast al eens opgevallen dat de generaties boven jullie niet per se slim en ijverig zijn. Neem Peter Fröhlich, docent aan de Amerikaanse universiteit Johns Hopkins. Al jaren gebruikt hij het volgende systeem om de cijfers van zijn studenten te bepalen: de beste student krijgt een tien en alle andere cijfers bepaalt hij aan de hand van dit cijfer. Dus als de beste student een score van tachtig punten heeft, dan krijg iemand met zestig punten een 7,5. Volgens Fröhlich werkte zijn systeem prima, tot studenten dit jaar op het idee kwamen om het te kraken. Niemand maakte het examen. Daarmee had de beste student een score van nul punten. En alle andere studenten ook. Fröhlich hield zich aan zijn woord en gaf de hele klas een tien. Hij blijft bij zijn manier van cijfers geven, al heeft hij inmiddels de regel toegevoegd dat hij studenten een onvoldoende mag geven als hij het idee heeft dat ze met zijn systeem lopen te fokken.

Kunnen jullie niet zoiets verzinnen bij het eindexamen? Het is natuurlijk jammer dat jullie als je niets invullen altijd een één krijgen. Maar wacht even, als alle leerlingen een één krijgen, dan komt het natuurlijk nooit meer goed met die hooguit vijfendertig procent onvoldoendes. Wat zouden ze dan doen met hun normering? Ik juich jullie toe als jullie dat eens testen. Het lastigste is dat jullie wel moeten zorgen dat echt iedereen meedoet, maar ik heb alle vertrouwen in jullie.

Boks!

Ionica

Deze column verscheen afgelopen weekend in de Volkskrant.

Beste Bert de Jong,

U vroeg mij of ik kan berekenen wat de kans is dat u geboren bent. Daarvoor hoef ik helemaal niet te rekenen. Gegeven dat u deze vraag stelt, schat ik deze kans op honderd procent (tenzij u een robot bent, dan heeft u mij mooi te pakken).

Ik krijg regelmatig dit soort vragen. Een andere lezer wilde weten wat de kans is dat bij zijn verwekking precies de juiste eicel en zaadcel bij elkaar kwamen. Een dame vroeg naar de kans dat ze haar man ontdekte op een foto in haar eigen baby-album. En op Twitter zocht iemand de kans dat niet één van zijn 550 Facebook-vrienden die dag jarig was.

Al deze dingen waren al gebeurd voor ik de vraag kreeg, dus ik kon steeds honderd procent antwoorden. Maar dat is natuurlijk niet wat u en de anderen van mij vragen. U wilt weten hoe bijzonder uw leven is. En u hoopt dat dit op de een of andere manier te berekenen is.

Wat is de kans dat iemand deze slechte grap verzint?

Er zijn verschillende manieren om kansen uit te rekenen: domweg tellen, handig deelkansen vermenigvuldigen of iets echt slims doen (al gaat dat laatste bij mij vaak mis). Voor de kans dat u geboren bent, moeten we vooral veel schatten. Wat is de kans dat uw ouders precies op het juiste moment de liefde bedreven en u als kind kregen? Laten we heel optimistisch zijn en die kans op vijftig procent schatten. Voor uw grootouders aan beide kanten zetten we de kans dat zij samen kwamen ook op elk vijftig procent. Zo gaan we terug de geschiedenis door tot we bij de eerste mensen komen die hier grofweg 200.000 jaar geleden rondliepen.

Stel nu even dat de gemiddelde leeftijd van moeders vijfentwintig jaar was, dan geeft dat in 200.000 jaar achtduizend moeders. Best een overzichtelijk aantal: iets meer dan de inwoners van Noord-Beveland aan mama’s. Als elk van die oermoeders vijftig procent kans had om op het goede moment door de bijpassende oervader bevrucht te worden, dan is de kans dat u geboren bent vijftig procent tot de macht achtduizend. Dat is ongeveer één op tien tot de macht 2.408, een kans zo belachelijk klein dat er geen woorden meer voor zijn. Het is waarschijnlijker dat u bij de lotto zes jaar lang elke week de jackpot wint.

Het is dus heel bijzonder dat u geboren bent. Maar voor u zichzelf tot het achtste wereldwonder kroont: uw vervelende buurman is net zo bijzonder. En die mug die u net wegjoeg had een nog veel kleinere kans om geboren te worden. Berekeningen helpen niet om te zeggen of iets bijzonder is. Er gebeuren doorlopend dingen die een extreem kleine kans hebben. Meestal merken we daar niets van, we denken er pas over na als er iets gebeurt dat wij bijzonder vinden. Het is zoals Terry Pratchett graag grapt: “Een kans van één op een miljoen komt negen van de tien keer uit.”

Succes,

Ionica

ps De kans dat op een bepaalde dag geen van die 550 Facebook-vrienden jarig is, is trouwens ruim twintig procent. Helemaal niet zo bijzonder.

Deze column verscheen zaterdag in de Volkskrant.

Het is bijna zover! De laatste schooldag met stunt en het eindfeest zitten erop, en de al dan niet verplichte examentrainingen in de laatste lesweken zijn achter de rug. Nu is het meivakantie en daarna begint het: het eindexamen. Het moment waar je al die jaren naar toe gewerkt hebt.

Dit jaar gaan de strengere examenregels in. Voor de kernvakken (wiskunde, Nederlands en Engels) mag je maximaal één 5 halen als eindcijfer. Voorheen kon je nog slagen met een 4 voor wiskunde als je voor alle andere vakken voldoendes had, waarvan minstens één 7. Of je kon voor zowel wiskunde als Nederlands een 5 halen, mits daar weer minstens één 7 en verder allemaal voldoendes tegenover stonden. Nu dus niet meer. Bovendien moet sinds vorig jaar het gemiddelde van alle centrale examens een 5,5 zijn, je kunt dus niet meer op je lauweren gaan rusten als je prachtige schoolexamencijfers hebt gehaald. De druk neemt toe!

Het slagingspercentage zal dus waarschijnlijk wat lager liggen dan eerdere jaren. Maar dat was natuurlijk niet het doel, de bedoeling was dat iedereen wat harder zou gaan werken en beter voorbereid naar het vervolgonderwijs zou gaan.

Ik zie echter dat jullie vooral dure, buitenschoolse examencursussen gaan volgen. Prima op zich: hoe meer je oefent, hoe beter het is. Maar overschat die cursussen niet! Jullie tellen massaal 300 euro neer voor iets dat je al kunt, of zou moeten kunnen. Je hebt al jaren geoefend, je hebt honderden toetsen gemaakt, de stof is herhaald, herhaald en nog eens herhaald. Je hebt op school de laatste weken alle tijd en ruimte gehad om oude examens te oefenen en om je docenten met vragen te bestoken. Docenten die al weten waar jouw zwakke plekken zitten, die weten waar jij van in paniek raakt.

Maar ik zie jullie denken: zo’n training is natuurlijk veel beter dan school! Daar betaal je zoveel geld voor, dat moet een garantie op succes zijn!

Als jullie op examencursus gaan, leer je soms een rekenmachinetrucje dat je niet van je docent geleerd hebt. Niet omdat je docent dat trucje niet kent, maar omdat je docent graag wil dat je snapt wat je doet. Een docent heeft een didactische opleiding gehad. Die voelt zich niet alleen verantwoordelijk voor jouw eindexamencijfer, maar ook voor jouw slagingskansen op je vervolgopleiding en voor je studievaardigheden in het algemeen. En daar heeft hij of zij zijn uiterste best voor gedaan!

Zo’n training kan nuttig zijn, als een eindspurtje. Gedwongen een boel extra uren in een vak stoppen, omdat je zelf niet genoeg discipline kunt opbrengen. Of omdat je te laat begonnen bent met werken. Maar die geweldige, gestructureerde samenvattingen? Die staan ook gewoon in je boek. En oude examens oefenen? Dat kun je thuis ook, ze staan allemaal op internet.

Dus ben je nog wat onzeker, maar ga je zo’n examentraining niet volgen, omdat je ouders het niet nodig vinden of omdat je het gewoon niet kunt betalen? Maak je vooral niet teveel zorgen! Je bent er eigenlijk al klaar voor.

Heel veel succes!
Jeanine (ook wel bekend als “mevrouw Daems”)

Deze column verscheen afgelopen weekend in de Volkskrant.

Beste prins Willem-Alexander,

Over enkele dagen bent u onze koning. In navolging van de bestseller Physics for Future Presidents geef ik u in deze brief een zeer korte samenvatting van Wiskunde voor toekomstige koningen. Alles wat u nodig heeft uit het mooiste vakgebied met de W (drie vingers in de lucht!).

Om mijn republikeinse collega Jeanine te paaien, verwijs ik met de titel van deze brief naar één van haar lievelingsboeken. En voor wie dat niet begreep, doe ik er ook nog een plaatje bij.

Allereerst is het cruciaal dat u goed overweg kunt met grote getallen. Even snel uit het hoofd: hoe groot is de totale Rijksbegroting van Nederland? Is dat ongeveer 190 miljoen, miljard, biljoen of biljard? En hoeveel procent van die begroting gaat naar de post “koning”? Tip: noemt u dat laatste percentage vooral als iemand moppert dat het koningshuis te duur is. Mocht u uzelf nog willen trainen in de omgang met grote en kleine getallen, dan raad ik u het boek Ongecijferdheid van John Allen Paulos aan.

Ten tweede lijkt het me zeer belangrijk dat u leugens in statistieken herkent. Veel mensen zullen u proberen te overtuigen van hun gelijk met indrukwekkende grafieken en gemiddelde cijfers. Wantrouw te mooie driedimensionale diagrammen en controleer altijd of er niet gesjoemeld is met de assen. Bedenk dat het gemiddelde soms weinig zegt. In een klas waar de helft van de leerlingen een tien haalt en de andere helft een twee, is het gemiddelde cijfer een zes.Wilt u zich tegen bedrog wapenen, lees dan vooral Darrell Huffs klassieker How to lie with statistics of de moderne variant Goochelen met getallen van mijn collega Hans van Maanen.

Belangrijker dan behendig omgaan met getallen is misschien nog wel het talent om helder en logisch te redeneren. Hopelijk kent u het verschil tussen correlatie en causaliteit en bent u voorzichtig als u conclusies trekt over oorzaak en gevolg. Er is voor mannen bijvoorbeeld een sterke correlatie tussen een lang leven en gehuwd zijn. Voordat u begint te juichen: dit betekent niet dat een huwelijk ervoor zorgt dat u langer leeft. Het is precies andersom: mannen met een hoge levensverwachting hebben een grotere kans om een vrouw te vinden.

Een andere logische fout die u hopelijk vermijdt is het onjuist omkeren van een “als dit, dan dat”-redenering. Stel bijvoorbeeld dat ik zeg: “Als ik wakker word, dan eet ik stamppot.” Dan betekent dat níet dat ik altijd net wakker ben als ik stamppot eet. Dat doe ik immers ook wel eens ‘s avonds. Dit soort redeneringen gaat vaak precies op deze manier mis. Alle boeken die ik in deze brief noem, geven voorbeelden van deze en andere denkfouten.

Tenslotte hoop ik dat u als koning uitdraagt dat wiskunde helemaal geen eng vak is en dat u uw drie dochters aanmoedigt om hun best te doen bij de exacte vakken. Als u nog mooie verhalen, leuke raadsels of knutselideeën zoekt, dan is, al zeg ik het zelf, Ik was altijd heel slecht in wiskunde echt iets voor u (de titel is niet autobiografisch, ik schreef het boek met Jeanine Daems). En mocht u ooit behoefte hebben aan een opfriscursus voor uzelf of bijles voor de prinsesjes, dan kom ik graag een keer naar uw paleis.

Uw onderdaan,

Ionica

Deze column verscheen afgelopen weekend in de Volkskrant.

Beste nieuwsgierige belegger.

De afgelopen weken stuurde je me heel wat vragen over bitcoins. Wat is dat nou voor munt? Moet je die kopen? Hoeveel zijn er eigenlijk in omloop? En wat is dat vage gedoe over de deelbaarheid van dit nieuwe geld?

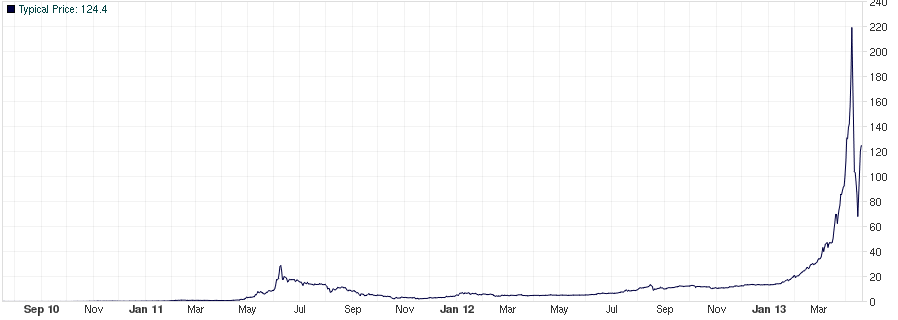
Laten we bij het begin beginnen. In 2008 bedacht Satoshi “niet zijn echte naam” Nakamoto een systeem om via internet betalingen te regelen zonder tussenkomst van een traditionele bank. Zijn bitcoins zijn dus een soort digitaal geld en het bijzondere is dat er geen bank of organisatie is die dit geld beheert. Transacties tussen gebruikers gaan niet via een centraal orgaan, maar worden in het netwerk gecontroleerd door een proces met codes en versleutelingen. Nieuw geld wordt “gemijnd” via ingewikkelde berekeningen die veel rekenkracht kosten. Zo is het vinden van een bitcoin net zo lastig als het opdiepen van goud uit een mijn. In theorie dan. Je kunt bitcoins ook gewoon kopen en verhandelen, net als andere valuta. En er zijn wereldwijd zeker vier winkels die ze accepteren. De koers van bitcoins schommelt nogal, op het moment dat ik dit typ is één bitcoin ongeveer zeventig euro waard.

Tikje wisselvallig, die koers van de bitcoin in dollars (klik voor een grotere versie).

Of het slim is om ze te kopen als belegging is een vraag die meer met economie dan wiskunde te maken heeft. Dat lijkt me meer iets voor Bas Haring. Daarom ga ik snel naar je laatste twee vragen, daar kan ik namelijk wel iets over zeggen.

Op dit moment zijn er ruim elf miljoen bitcoins op de markt, de waarde van alle bitcoins bij elkaar is daarmee ongeveer 770 miljoen euro. Dat is ongeveer 0,1 procent van wat er aan eurobiljetten in omloop is. Facebook kocht voor dit bedrag Instagram (al ging die betaling nog gewoon in dollars). Bill Gates kan alle bitcoins in één keer opkopen met een fractie van zijn vermogen. Erg veel zijn het er dus nog niet. Het merkwaardige is dat er een harde grens zit aan het aantal bitcoins dat er uiteindelijk komt. Per jaar komt er een vastgesteld aantal uit de digitale mijnen tot er in 2140 iets minder dan 21 miljoen bitcoins zijn. Daarna komen er geen meer bij.

Is dat wel genoeg? Bij normale valuta kan een bank beslissen dat er meer geld nodig is. De bitcoins zijn op een gegeven moment gewoon op. Daar komt precies die deelbaarheid bij kijken. Bij een betaling in euro’s gaan we niet verder dan in centen (en bij veel winkels gaan de betalingen niet verder dan tot op de vijf cent). Maar bij digitale betaling zou je prima met 0,00000001 cent kunnen werken. Dat is precies wat bitcoins doen. Deze munt bestaat uit honderdmiljoen centen. Je kunt in de toekomst dus werken met milibitcoins of microbitcoins. Het totale aantal daarvan zou ruim voldoende moeten zijn. In theorie dan.

Het is de bedoeling dat de bitcoin flink meer waard wordt, zodat die kleine eenheden handig worden bij betalingen. Hoe dát precies moet gebeuren is mij nog steeds een raadsel. Zolang ik dat niet snap, ga ik mijn spaargeld nog maar niet omruilen voor bitcoins.

Succes,

Ionica

Deze column verscheen afgelopen weekend in de Volkskrant Met dank aan mijn onvolprezen boekhouder Marina Clausing die meedacht over de juiste vergelijking..

Beste congres-organisatie,

Wat leuk dat jullie me vragen voor een lezing, natuurlijk kan ik een verhaal vertellen over onverwachte toepassingen van wiskunde! Het is alleen jammer dat jullie geen budget hebben voor sprekers. Jullie boeken voor je congres een prachtig landgoed, huren een dure cateraar, maar de inhoud moet bijna gratis komen. Dat is toch merkwaardig. Ik kan als zelfstandige geen lezing komen geven voor 150 euro. Ik zal nog één keer uitleggen wat een fatsoenlijk tarief is.

Zie mij eens lekker staan op dat podium.

Laten we eens kijken naar wat iemand in loondienst kost. Neem mijn oude studievriend Bert, hij verdient 3.600 euro bruto per maand. Dat is bovenmodaal, maar voor onze werkervaring en opleidingsniveau onder het gemiddelde. Voor zijn werkgever komen er bovenop dat brutoloon nog werknemersverzekeringen, sociale premies en vakantiegeld. Bij elkaar zijn de werkgeverskosten ongeveer 59.000 euro per jaar. En dan heb ik de bonus van Bert nog niet eens meegeteld.

Bert heeft ook een mooie werkplek, een telefoon, laptop plus een hele lading kantoorspullen van de zaak en hij mag diverse onkosten declareren. Moet hij naar een vergadering in Sneek? Zijn baas betaalt de reiskosten, eten onderweg en als het nodig is een hotel. Zeg dat al dit soort kosten nog eens zesduizend euro per jaar zijn. Dan komen we voor een werkgever op 65.000 euro aan kosten.

Hoeveel kost Bert daarmee per uur? Hij werkt full-time, maar lang niet al zijn uren zijn declarabel. Hij maakt regelmatig eens praatje bij de koffie-automaat of zit even voor zich uit te staren. Verder zijn er vergaderingen, cursussen, het beantwoorden van talloze emails, het oplossen van computerproblemen en al die andere dingen die naast zijn eigenlijk werk moeten gebeuren. Daarnaast gebruikt Bert zijn volle zesentwintig vakantiedagen en ligt hij wel eens met griep in bed. Zeg dat hij uiteindelijk duizend uur declarabel werk per jaar overhoudt. Dan kost Bert zijn werkgever uiteindelijk per uur 65 euro. Uit betrouwbare bron weet ik dat Bert het dubbele kost als hij eens aan een ander bedrijf wordt verhuurd.

Het lijkt me dus zeer redelijk dat ik als zelfstandige 65 euro per gewerkt uur reken. Op het eerste gezicht houd ik meer geld over dan Bert, maar ik heb veel meer onzekerheid en kosten dan hij (en leuker werk, dat dan weer wel). Mijn arbeidsongeschiktheidsverzekering is duurder dan die van een werknemer en pensioen moet ik op een of andere manier zelf opbouwen. Verder gaan opdrachtgevers wel eens failliet of krijg ik een tijdje domweg geen opdrachten terwijl Berts loon elke maand binnenkomt. Kortom: 65 euro per uur is echt het minimum.

Probeer nu eens te schatten hoeveel tijd een lezing op jullie conferentie me kost. Ik moet de vorm en inhoud met jullie overleggen, de juiste voorbeelden opduiken, een presentatie maken en oefenen. Op de dag zelf kom ik naar jullie afgelegen landgoed (in totaal vijf uur reizen), ben ik een uur van tevoren aanwezig om de techniek te testen en blijf ik op verzoek van jullie nog tot na de pauze zodat ik vragen kan beantwoorden. Na afloop stuur ik jullie netjes mijn presentatie en aanvullende informatie voor de deelnemers. Alles bij elkaar kost dit me makkelijk twee complete dagen. Reken zelf maar even uit voor welk bedrag jullie me kunnen boeken.

Hopelijk tot ziens,

Ionica

ps Zoals ik al schreef is 65 euro per uur het absolute minimum. Niet schrikken als ik af en toe wat meer vraag dus.

Deze column verscheen afgelopen zaterdag in de Volkskrant.

Beste Elise Andrew,

Om te beginnen: complimenten voor je geweldige Facebookpagina “I fucking love science”! Een aanrader. (Voor mensen die niet van schuttingtaal houden: zie de afgeleide pagina “Science is awesome”.) Ik volg je al tijden. Elke dag verschijnen er mooie foto’s van rare insecten, hilarische nerdgrappen en toegankelijke wetenschapsnieuwtjes. Van medische doorbraken tot sterrenkunde, van nanodeeltjes tot prehistorische fossielen. Heerlijk, als pauze tussen het lesgeven door. En dat vinden meer dan vier miljoen andere internetters ook.

Vorige week meldde je je aan op twitter. Leuk, nog meer nieuwtjes! Je plaatste dus argeloos op je site een linkje naar je twitteraccount. Onder je eigen naam, met (jawel!) een foto van jezelf. Een leuke, jonge vrouw. En de hel brak los. Binnen een paar minuten verschenen er bergen verbaasde reacties. Niet omdat je nu ook twittert, maar omdat je, nou ja, een aantrekkelijke vrouw bent. Die over wetenschap schrijft. En een woord als “fucking” bezigt. Hoe bijzonder.

Je kreeg een paar soorten vaak terugkerende reacties. Type één: verbazing. Uitspraken als: “Holy shit, I had no clue you were a woman!” en “Always thought you were a dude, I feel like my world has been turned upside down hahah”. Type twee, vooral door mannen: de focus op je uiterlijk. “She has the brains AND the looks!!!??? I am in love.” En type drie: reacties van mensen die de site nog toffer vinden nu ze weten dat hij door een vrouw gemaakt wordt. Ook best raar.

Je kunt zeggen: nou, er werken gewoon niet zoveel vrouwen in de bètawetenschappen, dus de kans dat de site door een man bijgehouden werd is gewoon veel groter. Oké. Maar dan nog zijn de reacties opvallend. Waarom is het zo’n schok? Alleen omdat het statistisch wat minder waarschijnlijk is? Bij mannelijke wetenschappers gaat het nooit direct over hun uiterlijk. Of botst jouw internetimago met allerlei ideeën die ook wij, hoogopgeleide jonge mensen, onbewust hebben over mannen en vrouwen? Zoals een verbaasde reageerder zegt: “meisjes vloeken niet en zijn vaak bang voor spinnen”.

Toevallig waart er ook door Nederland een nieuwe feminismediscussie, nadat omroepbaas Shula Rijxman bij De Wereld Draait Door redacties van praatprogramma’s opriep om eens wat vaker een deskundige vrouw te bellen. Want 70 procent van de gasten zijn mannen, dat is geen goede afspiegeling van de maatschappij. En om ze op weg te helpen (want wat is makkelijker dan steeds dezelfde mensen bellen) had zij vast een lijst van deskundige vrouwen gemaakt, op een presenteerblaadje. Zoals de BBC laatst ook gedaan heeft.

Maar, werd ook gezegd: slimme vrouwen willen eigenlijk liever niet op tv. Alleen als ze vanwege hun specifieke deskundigheid op een bepaald gebied gevraagd worden. Terwijl mannen sneller denken dat ze ergens verstand van hebben. Ook generaliserend, maar ik zelf herken dat wel.

Jij niet, gelukkig. Je wordt overal uitgenodigd vanwege deze gebeurtenis, je laat jezelf zien, prima! Voor je het weet zit jij straks in de database van de BBC, en vragen ze je ook vanwege je expertise. Zodat de wetenschap er een realistisch rolmodel bij heeft.

Keep up the good work!

Jeanine

Deze column verscheen afgelopen weekend in de Volkskrant. In de online versie van de vorige column waren de kansen waarnaar deze brief verwijst al verbeterd.

Beste Ionica,

Wekelijks lezen jij en je collega Jeanine Daems iemand de les die een wiskundig foutje maakt. Als wiskundemeisjes leggen jullie nog één keer uit hoe het wel moet. Als lezer verwacht ik daarom dat je zelf uiterst zorgvuldig bent in je redeneringen.

Vorige week besprak je de loting voor de kwartfinales van de Champions League. Die viel zo uit dat van de acht teams “de grote vier” in vier verschillende finales belandden. Je legde aan Johan Derksen uit wat de kans is op zo’n verdacht handige loting. Om dat uit te rekenen, geef jij bij de loting elk team een getal tussen de één en acht. In de eerste kwartfinale speelt team één tegen team twee, in de tweede team drie tegen team vier, enzovoorts. Vervolgens beweer je dat “de grote vier” elkaar ontlopen als ze allemaal een even nummer krijgen óf juist allemaal een oneven nummer. Daarna laat je het telwerk aan de lezer over en komt al handenwapperend op een kans van één op vijfendertig.

Alleen is het een beetje dom dat je vergeet dat de vier teams ook niet tegen elkaar spelen als ze bijvoorbeeld posities één, vier, vijf en zeven loten. En zo zijn er nog veel meer mogelijkheden. Om precies te zijn: acht keer zoveel. De juiste kans is dan ook acht op vijfendertig.

Jij nam je berekening over van een andere wiskundige, maar dat is natuurlijk geen excuus. Als je het altijd allemaal zo goed weet, dan mag je best even controleren of wel klopt wat je opschrijft. Ik zal nog één keer uitleggen hoe dat in dit geval had gekund. Als we beginnen met het eerste team, dan kan dat nog alle acht vrije nummers krijgen zonder dat het één van de andere “grote” teams tegenkomt. Voor het tweede grote team zijn er nog zeven plekken vrij en de kans is dat zij bij de loting het eerste team ontwijken. Het derde team heeft nog zes open plekken en op vier daarvan hoeven ze niet tegen de eerste twee teams te spelen. Tenslotte zijn er voor het vierde team nog vijf plekken over, waarvan twee plekken niet tegen de andere groten. Kortom: de kans op een loting waarbij de grote vier elkaar ontwijken is .

Terug naar school, Ionica Smeets!

Alle andere kansen in je column kloppen door jouw fout ook niet. De kans op een loting zoals Johan Derksen hem beschreef is ruim elf procent. En als hij voor de loting de kans op doorgestoken kaart op vijfentwintig procent schatte, dan stijgt die kans na deze uitslag naar bijna vijfenzeventig procent. Graag gedaan hoor wiskundemeisje, het was een kleine moeite om het even goed uit te rekenen.

Het enige excuus dat je hebt, is dat kansrekenen notoir lastig is. Een onjuiste redenering klinkt vaak heel plausibel. Martin Gardner schreef eens dat er geen ander gebied van de wiskunde is waar experts zó makkelijk kunnen blunderen. Maar lieve Ionica, je mag voortaan best iets milder zijn voor anderen die eens een foutje maken met wiskunde. Wie zonder zonde is, enzovoorts. Misschien moet je eens wat kritischer naar jezelf kijken.

Groeten van jezelf,

Ionica