Wiskundemeisjes
Archief voor categorie 'Trivia'
Dick stuurde ons weer een goede link! Op de site van Sanny de Zoete vond hij deze geweldige priemgetalservetten:

Wat is er nou zo bijzonder aan deze servetten? De blokjes in het patroon hebben te maken met priemgetallen. De servetten zijn gebaseerd op het volgende patroon, dat Balthasar van der Pol in de jaren '50 ontwierp.

De blokjes in het patroon stellen niet precies de gewone priemgetallen voor, maar de priemgetallen in de gehele getallen van Gauss. De gehele getallen van Gauss zijn de getallen die je kunt schrijven als a+bi, waarbij a en b gehele getallen zijn en waarbij we stellen dat i2=-1. Met deze getallen kun je net zo rekenen als met gewone gehele getallen.
Ook kun je priemgetallen definiëren in deze nieuwe verzameling getallen. De gewone priemgetallen zijn gedefinieerd als: een priemgetal is een getal met precies vier delers. Het priemgetal 3 heeft bijvoorbeeld 1, -1, 3 en -3 als delers. (Merk op dat bijvoorbeeld -3 volgens deze definitie ook een priemgetal is.) Een equivalente definitie is: p is een priemgetal als geldt: als x en y getallen zijn zodat p een deler is van xy, dan is p een deler van x of van y. Deze tweede definitie kunnen we precies zo overnemen in de gehele getallen van Gauss.
Het blijkt dat alle gewone priemgetallen die bij deling door 4 rest 3 opleveren, nog steeds priem zijn. Dus als p een gewoon priemgetal is dat rest 3 geeft bij deling door 4, dan is p = p+0i een priemgetal in de gehele getallen van Gauss. De getallen 3, 11 en 19 blijven dus priem. Maar de gewone priemgetallen die bij deling door 4 rest 1 opleveren, zijn nu niet meer priem! Het is namelijk zo dat priemgetallen van dit type allemaal te schrijven zijn als een som van twee kwadraten. Bijvoorbeeld: 5=22+12, 13=32+22, 17=42+12. Maar p=a2+b2 is te onbinden als (a+bi)(a-bi), dus in de gehele getallen van Gauss is een gewoon priemgetal dat rest 1 geeft bij deling door 4 niet meer priem. Het blijkt dat in dit geval a+bi en a-bi wel priemgetallen zijn, en de getallen a+bi en a-bi vermenigvuldigd met -1, i of -i ook. Een dergelijk priemgetal a+bi heeft precies acht delers in de gehele getallen van Gauss: a+bi, -a-bi, -b+ai, b-ai en de triviale delers 1, -1, i en -i.
Merk op dat een getal dat rest 0 geeft bij deling door 4 sowieso nooit priem is, en dat 2 het enige priemgetal is dat rest 2 heeft bij deling door 4. Het priemgetal 2 is in priemfactoren te ontbinden als (1+i)(1-i), dus 2 is ook niet meer priem in de gehele getallen van Gauss.
Samengevat: de gewone priemgetallen die rest 3 geven bij deling door 4 blijven priem, de priemgetallen die rest 1 geven bij deling door 4 ontbinden als (a+bi)(a-bi) waarbij a en b gehele getallen zijn zodat a2+b2 dat gewone priemgetal is, en het gewone priemgetal 2 heeft in de gehele getallen van Gauss de priemontbinding (1+i)(1-i).
Maar vinden we op deze manier alle priemgetallen van Gauss? Dat blijkt zo te zijn. Voor elk priemgetal van Gauss a+bi dat niet gelijk is aan p, -p, pi of -pi, met p een gewoon priemgetal, geldt dat a2+b2 wel een gewoon priemgetal is. Alle priemgetallen van Gauss komen dus op de een of andere manier voort uit de gewone priemgetallen.
Hoe staan de priemgetallen van Gauss nu in het servet? Het middelste hokje stelt (0,0) voor. Het hokje (a,b) wordt nu blauw gekleurd als a+bi een priemgetal van Gauss is, en anders blijft het wit. Lees hier de uitleg van Balthasar van der Pol zelf.
Oftewel: op de horizontale en verticale assen staan de getallen (0,p), (0,-p), (p,0) en (-p,0), waarbij p een gewoon priemgetal is dat bij deling door 4 rest 3 geeft. Op alle andere plekken staan de getallen (a,b) waarvoor geldt dat a2+b2 een gewoon priemgetal is dat óf gelijk aan 2 is, óf bij deling door 4 rest 1 geeft.
De dekservetten kosten 15 euro per stuk en je krijgt er een brochure met uitleg over de priemgetallen op het doek bij.
(Jeanine)
Arjen stuurde ons een link naar de volgende foto:

Weet iemand van jullie wat de uitkomst betekent?!
(Jeanine)
Elke wiskundige en wiskundestudent kent ze: de gele wiskundeboeken van Springer. (Een vriend van mij heeft wel eens gevraagd of ik wiskunde was gaan studeren omdat ik dan veel gele boeken kon kopen; geel is namelijk mijn lievelingskleur.)
Als je een wiskundige wil leren kennen, kun je natuurlijk kijken welke Springer-boeken hij heeft en daar je conclusies uit trekken. Maar via Koen vonden we een leuke test waaruit je kunt opmaken welk Springer-boek je bent (of eigenlijk: zou zijn als je een Springer-boek was). Laat je collega's de test doen en je weet wie/wat ze zijn!
Aangezien Koen nieuwsgierig is en graag wil weten welk boek wij zijn, hebben wij de test ook gedaan.
Jeanine blijkt een leuk boek te zijn dat ze inderdaad ook heeft:
 |
If I were a Springer-Verlag Graduate Text in Mathematics, I would be Saunders Mac Lane's Categories for the Working Mathematician. I provide an array of general ideas useful in a wide variety of fields. Starting from foundations, I illuminate the concepts of category, functor, natural transformation, and duality. I then turn to adjoint functors, which provide a description of universal constructions, an analysis of the representation of functors by sets of morphisms, and a means of manipulating direct and inverse limits. |
En Ionica is:
 |
If I were a Springer-Verlag Graduate Text in Mathematics, I would be J.-P. Serre's Linear Representations of Finite Groups. My creator is a Professor at the College de France. He has previously published a number of books, including Groupes Algebriques et Corps de Classes, Corps Locaux, and Cours d'Arithmetique (A Course in Arithmetic, published by Springer-Verlag as Vol. 7 in the Graduate Texts in Mathematics). |
De grote vraag is nu natuurlijk: welke boeken zijn jullie, lieve lezers?
(Jeanine)
Wie heeft er nooit last van: je hebt dringend een heel mooie, haast perfecte cirkel nodig. En precies dan is er geen passer in de buurt en er zit ook geen mooi rond muntje in je portemonnee. Of nog erger: je staat voor een schoolbord, en bordenpassers zijn nog schaarser dan gewone passers (in ons gebouw in elk geval wel, daar schijnt er één te zijn, maar slechts enkele medewerkers weten waar).
Er zijn mensen die daar een andere oplossing voor gevonden hebben: die kunnen Heel Mooie cirkels tekenen, met de hand, op een schoolbord. Op YouTube is een heuse rage ontstaan, die begon met het onderstaande filmpje van een wiskundeleraar met gevoel voor humor.
De leraar in kwestie is Alexander Overwijk uit Ottawa, Canada. Elk jaar tekende hij een bijna perfecte cirkel op het bord en vertelde hij zijn leerlingen het verhaal van het wereldkampioenschap freehand circle drawing, dat helemaal niet waar was. In dit krantenartikel lezen we:
"It's my schtick with my kids. I've been telling them this story for 10 years," Mr. Overwijk, a 17-year veteran math teacher, said Friday. Mr. Overwijk stopped using a compass nearly a decade ago to draw circles because "it was just a pain."
As a joke, he told his students that he was the freehand circle champ in Las Vegas, having watched the bartending championships the weekend before. "It just spewed out and most of the class bought it," he says, adding that he's done the act every year since.
Vorig jaar werd deze act gefilmd door een leerling en het filmpje kwam op YouTube terecht. Het resultaat: nog meer cirkels tekenende mensen op YouTube, zie bijvoorbeeld deze filmpjes.
Maar al deze publiciteit leverde ook veel animo op voor een echt kampioenschap. Iedereen kon meedoen voor $5 en de opbrengsten zijn voor een goed doel. En wie was de winnaar? Juist!
(Jeanine, met dank aan Dick voor de tip)
Dankzij Easter Eggs ontdekte ik dat er in mijn favoriete programmeer-tool Matlab een paar verrassingen zitten. Probeer bijvoorbeeld eens 'penny' in te typen als commando en bewonder het resultaat. Niet alle Easter Eggs werkten bij mijn versie, maar wie weet doen ze het bij jullie wel.
De mooiste verrassing vind ik het commando 'spy'. Dit is een keurig gedocumenteerd commando, dat voor een gegeven matrix laat zien welke elementen ongelijk zijn aan nul. Maar wat krijg je als je 'spy' typt zonder argumenten? Dit geweldige plaatje!
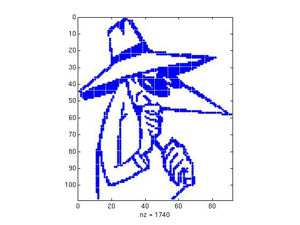
(Ionica)
ps Voor wie vroeger (onterecht) niet de Mad las, zie ook de Spy vs Spy Gallery.
Morgen is het Valentijnsdag. Iedereen die nog op zoek is naar een goed idee voor een wiskundige Valentijnskaart kan zijn of haar hart ophalen op de site van Jürgen Köller: Heart Curve.

Daar kun je zien hoe je op wiskundig verantwoorde wijze het allermooiste hartje zelf kunt tekenen. Of welke functie je je Valentijn moet sturen, zodat de gelukkige zelf het hart kan reconstrueren!

Als je ook op wiskunde vertrouwt als je je afvraagt of je je Valentijnskaart wel naar de juiste persoon stuurt, lees dan Wiskunde voorspelt huwelijkscrisis op Kennislink.
(Jeanine)
Laatst kregen we twee tips over dezelfde website binnen in dezelfde week. Arjen tipte ons over de hele site van Plus Magazine en Michiel stuurde ons naar een speciaal artikel over 6174. We zijn dol op gekke feitjes over getallen en zetten graag 6174 even in het zonnetje.

In 1949 bedacht de Indiase wiskundige Kaprekar het volgende algoritme:
- Schrijf een getal van vier cijfers, waarbij de cijfers niet allemaal hetzelfde zijn.
- Herschik de cijfers om het grootste en het kleinste getal te maken wat je met deze vier cijfers kunt maken.
- Trek het kleinste getal af van het grootste en ga terug naar stap 2 met de uitkomst.
Hoe komt die man erop? Nuja, welwillend proberen we het algoritme op 1729, ons favoriete getal van vier cijfers.
9721 - 1279 = 8442
8442 - 2448 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
(nog heel even volhouden)
8532 - 2358 = 6174
7641 - 1467 = 6174
(enzovoorts hierna).
Als je eenmaal op 6174 komt, dan blijft dat getal zichzelf herhalen. En nu komt het echt mooie: elk getal van vier cijfers (behalve 0000, 1111, ..., 9999) komt uiteindelijk op 6174 uit. Hoera voor 6174! Wie wil weten waarom en hoe dit gaat met getallen van meer cijfers, kan het uitgebreide artikel op de mooie site van Plus Magazine lezen of de Kaprekar generator downloaden.
(Ionica)
Jeffrey Shallit schreef over een leuke truc met priemgetallen. Schrijf een willekeurig priemgetal op. Streep nu een aantal cijfers van je priemgetal door, je mag ook nul cijfers wegstrepen. Op deze manier kun je van elk willekeurig beginpriemgetal een priemgetal uit de volgende lijst maken:
2, 3, 5, 7, 11, 19, 41, 61, 89, 409, 449, 499, 881, 991, 6469, 6949, 9001, 9049, 9649, 9949, 60649, 666649, 946669, 60000049, 66000049, 66600049.
Vinden jullie dit ook zo mooi? Shallit maakte kaarten die je kunt gebruiken om op feesten en partijen indruk te maken met je priemgetallen-manipuleer-skills.

In dit artikel (van maar vier bladzijden) bewijst Shallit zijn bewering en geeft hij een vergelijkbaar rijtje voor samengestelde getallen. Het rijtje dat hij geeft is minimaal in de zin dat als je een priemgetal p uit een priemgetal q in het gegeven rijtje kan maken door een aantal cijfers (nul is ook een aantal) weg te strepen, dat dan moet gelden p = q.
(Ionica)
Een tijdje terug kregen we twee emails over hetzelfde filmpje binnen. Zowel Martin als Arjan stuurden ons een link naar Math Lesson: A new way to multiply.

De methode die gebruikt wordt is helemaal niet zo nieuw, maar het ziet er mooi uit én het is leuk om te bedenken waarom dit werkt.
(Ionica)
 Internetbureau Rotterdam
Internetbureau Rotterdam 

