Wiskundemeisjes
Archief voor categorie 'Trivia'
Bart stuurt ons vaak wiskundige nieuwtjes, deze week kwam hij met een onderzoek uit Cambridge. Een studentenkrantje hield een seksonderzoek onder de studentenpopulatie en raad eens bij welke studie je het hoogste percentage maagden vindt? Jawel, het is wiskunde... Bijna de helft van de wiskundestudenten in Cambridge is nog nooit met iemand naar bed geweest. Een andere grappige uitkomst van het onderzoek:
Students at poorly-performing colleges are more likely to have high average levels of sexual partners.
Lees zelf het complete artikel Penetrating questions (pdf).
Bij deze roepen we onze lezers en vooral lezeressen op: ga eens naar bed met een wiskundige!

Dit weekend zijn mijn vriend en ik verhuisd (en Jeanine verhuist komend weekend, dus het zijn drukke tijden voor de wiskundemeisjes). We wilden in onze nieuwe woonkamer een mooi wiskundig patroon leggen met tapijttegels. Uiteindelijk hebben we een Sierpinski tapijt gelegd. Ik ben zo trots op het resultaat dat ik het aan jullie wil laten zien.


Zoals de kenners gelijk zullen zien is dit slechts de tweede iteratie van het Sierpinski tapijt. Na een boel iteraties krijg je een mooie fractal:

Jammer genoeg is onze woonkamer te klein voor meer iteraties en waren er geen vrijwilligers om de tapijttegels in kleinere vierkanten te snijden...
Dolf tipte ons over Random.org waar je sinds 1998 terecht kunt voor al je willekeurige getallen. Handig! Hierbij een reeks echt random getallen:
49 32 28 6 84 79 44 42 25 51 89 10 33 58 53 78 16 99 64 1 91 5 38 81 98 57 45 31 82 96 95 36 20.
Lees op de site vooral hoe ze de random getallen maken uit achtergrondruis en waarom het moeilijk is om met een computer echt willekeurige getallen te maken. Ik herhaal nog een keer deze leuke grap van Dilbert...

In het kerstnummer van NewScientist stond een leuk artikel over het spel Steen, papier, schaar. Je speelt met zijn tweeën: je telt af en dan maak je allebei tegelijk met je hand een steen (vuist), papier (vlakke hand) of schaar. Ik leerde vroeger op het schoolplein dat papier wint van steen, omdat je een steen in papier kan pakken. Steen wint van schaar, omdat je met een steen een schaar kan slijpen. En schaar wint natuurlijk van papier.
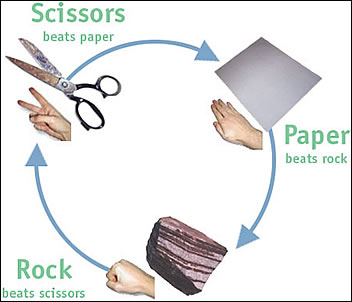
Je kunt het spel online spelen. Er blijken allerlei strategieën te bestaan en er is zelfs een heuse World RPS Society (professionals noemen het spel RPS of RoShamBo). Voor wie meer van programmeren dan van besliskunde houdt: er worden ook wedstrijden voor computerprogramma's gehouden. Al lijkt de laatste wedstrijd in 2001 te zijn gehouden...
Het artikel uit NewScientist is niet gratis toegankelijk, maar bij mental_floss vond ik online het soortgelijke How to Win at Rock-Paper-Scissors (and also how to cheat).
Twee tips van lezers over wiskunde en vooral liefde. Franka wees ons op Love plus one, over datingbureaus die wiskundige formules gebruiken om partners bij elkaar te brengen. Ik heb daar (net als de schrijfster van het artikel) weinig vertrouwen in. Maar misschien moeten de wiskundemeisjes toch eindelijk eens het door Vincent bedachte datingbureau flirt with a nerd oprichten.

Edward stuurde ons alweer een tijdje geleden The calculus of saying "I love you" met de geweldige ondertitel "Why you should never date man who knows more math than you." Jammer genoeg stelt het stukje wiskundig gezien niet erg veel voor, maar het idee om de liefde als een grafiekje te tekenen spreekt me wel aan. Ik mis alleen deze:

Zowel het liedje als het filmpje zijn fantastisch! Voor alle wiskundigen: blijf luisteren tijdens de aftiteling. Met dank aan Tom Koornwinder die de link doorstuurde.
Voor beginners: pi uitgerold.

Voor gevorderden: keer een bol binnenstebuiten (met dank aan Rogier voor de tip).
Vorige week vroeg ik jullie: wat is de mooiste rechthoek?

Op het moment dat ik dit schrijf, hebben er 485 mensen gestemd en is dit de top 3:
- Rechthoek 8 (met 94 stemmen)
- Rechthoek 11 (met 72 stemmen)
- Rechthoek 10 (met 68 stemmen) .
Het plaatje en het idee kwamen van MathTrek. In hun artikel staat dat rechthoek 11 verhoudingen heeft die het dichtste bij de gulden snede liggen. Als eigenwijze wiskundige heb ik het plaatje vergroot, geprint en opgemeten met mijn geodriehoek. Misschien komt het doordat ik de zwarte lijntjes meeneem, maar ik kom op een andere guldenste rechthoek.
De gulden snede is gelijk aan (√5+1) /2, wat ongeveer 1,62 is. Dit is mijn gemeten top drie van meest gulden rechthoeken.
- Rechthoek 1 met verhouding 1,62
- Rechthoek 11 met verhouding 1,58
- Recthoek 3 met verhouding 1,67.
De grote favoriet rechthoek 8 heeft als verhouding 1,71 en rechthoek 10 zit helemaal ver van de gulden snede af met een verhouding van 1,86.
Wat kunnen we nu concluderen? Eigenlijk nogal weinig. De verschillen in de verhoudingen zijn erg klein en meetfouten spelen ongetwijfeld ook nog een rol. Uit de literatuur over de gulden snede hypothese (het vermoeden dat mensen de gulden snede als mooiste kiezen) begreep ik, dat de resultaten van dit soort onderzoek sterk afhangen van de uitvoering van het onderzoek.
Ik vind het wel grappig dat rechthoek 4 zo impopulair is, terwijl zijn verhouding (1,91) dichtbij die van rechthoek 10 ligt. Blijkbaar vinden we liggende rechthoeken mooier...
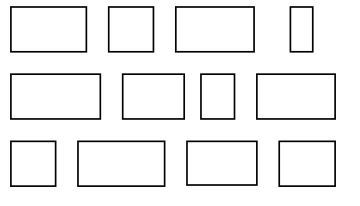
Wat vinden jullie de mooiste rechthoek? Voor het gemak heb ik de rechthoeken hieronder genummerd.

[poll=6]
Zoals jullie misschien al raadden: één van deze rechthoeken heeft verhoudingen die dicht bij de gulden snede liggen. Ik vroeg me af of mensen die nou echt mooier vinden. Later deze week zal ik vertellen welke de gulden rechthoek is!
 Internetbureau Rotterdam
Internetbureau Rotterdam 

