Wiskundemeisjes
Archief voor categorie 'Trivia'
Wat een rare titel! Inderdaad, de woorden autologlief, autologlyfe en de meervoudsvormen daarvan gaven vóór ik dit stukje typte nul google-hits. Maar het zijn de voor de hand liggende Nederlandse versies van het woord autologlyph. (Mijn groene boekje, ook niet meer de jongste, geeft zowel hiëroglief als hiëroglyfe, dus laten we voor dit nieuwe woord ook de opties nog even open houden.)
Het woord autologlyph is bedacht door Henry Segerman, die ook de mooie shirts gemaakt heeft waar we al eens over schreven. Een autologlief is een woord dat zo getekend is, dat het woord ook zelf is wat het betekent. Zoals wel vaker het geval is, is dit begrip beter duidelijk te maken aan de hand van wat interessante voorbeelden. Onderstaande autologliefen zijn allemaal afkomstig van Henry Segermans autologliefenwebsite.



Als je niet weet wat al deze Engelse wiskundewoorden precies betekenen, klik op een van de volgende links: fractal, mirror symmetry (= spiegelsymmetrie), wegsamenhangend (= path connected), enkelvoudig samenhangend (=simply connected), dicht (= dense), convergentie (= convergence), een artikel over de promotie van Chris Zaal waarin gladde krommen ter sprake komen op Kennislink (glad = smooth), star-shaped polygon (= stervormige veelhoek).
Maar de autologlief waar ik het meest van onder de indruk ben is deze:
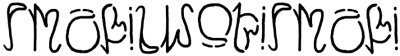
Dit is een heel bijzondere autologlief. Print dit woord (er staat anderhalf keer Möbius strip) op een transparantje en knip het uit. Maak er een Möbiusband van door het ene uiteinde één slag te draaien en dan vast te plakken aan het andere uiteinde. (Zie hier.) Op die manier ontstaat een Möbiusband waarop drie keer het woord Möbius strip te lezen is, terwijl je het maar anderhalf keer hebt afgedrukt! Ik heb er nog geen gemaakt om het te controleren, maar Segerman zelf gelukkig wel:

Edit: per abuis stond er overal autoglief in plaats van autologlief, dat is nu verbeterd, met dank aan JJ.
Sommige dingen zwerven al maanden op mijn laptop, vandaar op deze woensdag een galore van slechte grappen over/met wiskunde. Als eerste een plaatje van Bizarro waarvan ik niet meer weet hoe ik eraan kom.

Dat ik (hardop!) moest lachen om het onderstaande filmpje zegt waarschijnlijk meer over mij dan over dit filmpje.
Ik dacht trouwens eerst dat dit een acteur was die een typetje speelde, maar Luis Anthony Ast biedt zichzelf serieus aan als video math tutor...
En als uitsmijter een grap voor de wiskundige fijnproevers. Wat is een anagram van banach-tarski?
Antwoord: banach-tarski banach-tarski
Door HJ geknipt uit de Volkskrant:

Al is mijn naam niet goed gespeld, we zijn het echt! In gesprek met Pieter van der Wielen. Vanavond op Hoe!Zo? Radio, ergens tussen 21 en 22 uur.
Het houdt niet op met de wiskunde-t-shirts! Zowel Edward als Camiel stuurde ons deze week een linkje naar de weblog Neatorama, waar in de store twee leuke "I ♥ Math" shirts te koop zijn!


Het bovenste plaatje spreekt voor zich (kijk anders eens naar deze oude Valentijnpost). Op het onderste plaatje zie je een Lorenz attractor. Volgens de beschrijving van het t-shirt:
This T-shirt is the perfect gift for the math geek in your life.
Be sure to say "My love for you is dynamic in a complex and non-repeating pattern" when you give the shirt.
(If you want to know, that's a Lorenz attractor, which was devised by Edward Norton Lorenz in 1963 to describe convection rolls in the atmosphere. Lorenz attractor is a 3-D structure showing the state of a dynamic system that evolves over time in a complex, non-repeating pattern. Most people describe its shape as like a butterfly, but I think it looks a little like a heart.
Actually, you already know about Lorenz - he coined the term "butterfly effect" to describe the chaotic model of the weather.)
Voor de mensen die andere wetenschappen leuker vinden dan wiskunde (tsja...): er zijn ook shirts voor liefhebbers van biologie, natuurkunde, enz.
Steven wees me op een interessant computerspel: Echochrome, dat in de winkel ligt voor de Playstation Portable. Het spel is tamelijk wiskundig van aard en neemt een loopje met perspectief. Uit de recensie op tweakers.net:
In Echochrome staat het ontdekken van het juiste perspectief centraal. Het puzzelspel ziet er bedrieglijk eenvoudig uit, maar kan verduiveld lastig zijn. Het uitgangspunt is heel simpel. Op het scherm is niets meer te zien dan een zwevende constructie van witte balken tegen een spierwitte achtergrond. De speler kan de hele constructie alle kanten op draaien, en daarmee is zo'n beetje de actie in het spel samengevat. Over de zwevende balken loopt de hoofdrolspeler uit het spel, de zogenaamde mannequin.
De regels doen denken aan het werk van Escher, waar mannetjes op allerlei onmogelijk verbonden trappen lopen:
- De wet van de perspectiefwijziging - als twee gescheiden looppaden elkaar lijken te raken, dan gebeurt dat ook.
- De wet van de perspectieflanding - als twee paden zich boven elkaar lijken te bevinden, dan bevinden ze zich daar ook.
- De wet van het perspectief-bestaan - als het gat tussen twee paden aan het zicht is ontrokken en de paden lijken met elkaar verbonden, dan zijn ze dat ook.
- De wet van de perspectiefverdwijning - als een gat aan het zicht is onttrokken, bestaat het niet.
- De wet van de perspectiefsprong - als een mannequin springt, landt hij op het vlak dat er zich boven lijkt te bevinden.
In het volgende filmpje kun je een beetje zien wat er gebeurt:
Ik heb het spel niet gespeeld, want ik ben niet zo'n liefhebber van computerspellen en heb dus zeker geen playstation, maar het ziet er leuk uit! Lees verder op tweakers.net als je wil weten wat het doel van het spel is en wat Paul Hulsebosch van het spel vindt.
Om niet alleen reclame te maken voor onze eigen shirts: Henry Segerman heeft ook een mooie site waar je wiskundige shirts kunt bestellen! Kijk op Math-Art T-Shirts.

Toen ik verder op zijn homepage zocht, vond ik ook nog iets grappigs. Voor de wiskundigen en wiskundestudenten onder onze lezers: een
"Hoe vaak heb ik deze fout nu al gemaakt"-turf-tabel. (Toen ik hem aan mijn kamergenoot liet zien, zette hij vreemd genoeg meteen een kruisje bij getting distracted.)
Frank mailde ons een tijdje geleden trots dat hij een binair horloge had gekocht: dit horloge, om precies te zijn. ThinkGeek heeft ze natuurlijk ook, net als binaire klokken.

Het binaire stelsel om getallen te schrijven werkt eigenlijk net als het gewone decimale stelsel, alleen gebruiken we in het decimale stelsel de cijfers 0 t/m 9 en machten van 10, terwijl je in het binaire stelsel alleen de cijfers 0 en 1 gebruikt en machten van 2. In het decimale stelsel staat 12 voor 1 x 10 + 2 x 1. Als je het getal 12 binair wil schrijven, dan schrijf je het als 1100, want 12 = 1 x 23 + 1 x 22 + 0 x 2 + 0 x 1. Als het 12.05 uur is, staat op het horloge dus op de bovenste regel 1100 en op de onderste 000101 (waarbij een 1 voor "lampje aan" staat, en een 0 voor "lampje uit").
Vorig jaar vroeg Alex ons tijdens een lunchvergadering: "Zeg wiskundemeisjes, kennen jullie soms deze reeks getallen?"
4 8 15 16 23 42 108
Jeanine en ik keken naar de getallen, toen naar elkaar en daarna weer naar de getallen. Wij konden er niets van maken, laat staan dat we konden voorspellen wat het volgende getal in de reeks was. Alex vertelde dat deze getallen een belangrijke rol speelden in Lost.

Wiskundig gezien konden we er weinig mee, maar we kenden natuurlijk wel de fabelhaftige On-Line Encyclopedia of Integer Sequences. Jeanine en ik surften snel naar die site en typten de reeks 4 8 15 16 23 42 108 in. En de encyclopedie bewees weer eens hoe ontzettend volledig ze is. Kijk zelf maar wat er verscheen!
Leverde Evil Mad Scientist Laboratories ons pas nog een prachtige handleiding voor mooie Sierpinski-oorbellen, nu hebben ze ook fractalkoekjes gebakken!

Uitleg met veel foto's is wederom te vinden op Evil Mad Scientist Laboratories. De vorige keer heeft *niemand* mooie oorbellen gemaakt voor Ionica. Gelukkig houden de wiskundemeisjes ook van koekjes, en deze passen natuurlijk heel goed bij Ionica's mooie tapijt!
(Met dank aan Maarten en Ed.)
Iedereen (en ik bedoel ook echt iedereen) kent de stelling van Pythagoras: a2 + b2 = c2. Maar waar stonden die a, b en c ook al weer voor? En hoe kon je die stelling nou bewijzen? Ik leerde op school dat de stelling van Pythagoras geldt voor rechthoekige driehoeken en dat de stelling zegt dat de som van de kwadraten van de rechthoekszijden precies het kwadraat van de schuine zijde is.

Er bestaan veel (en ik bedoel ook echt veel) bewijzen van de stelling van Pythagoras. Op Cut The Knot staan er bijvoorbeeld zevenenzeventig. Zelf vond ik dit plaatje altijd een erg mooi bewijs geven.

De oppervlakte van het grote vierkant is (a+b)2 = a2 + 2ab + b2. Maar je kunt de oppervlakte van het grote vierkant ook schrijven als de som van het kleine vierkant en vier driehoeken: c2 + 4 x 1/2 x ab = c2+2ab. En hieruit volgt dat a2+b2=c2. Maar snap je na dit bewijs nu ook echt wáárom die relatie geldt? Ik eigenlijk niet.
Gelukkig is er BetterExplained, een site vol met betere verklaringen (en dan bedoel ik ook echt beter). In Surprising Uses of the Pythagorean Theorem geeft Khalid Azad een heldere uitleg. Elke rechthoekige driehoek kan in twee kleinere rechthoekige driehoeken verdeeld worden (in het plaatje is gekozen voor a = 3, b = 4 en c = 5, maar het geldt natuurlijk altijd).

Lees de rest zelf op BetterExplained en ontdek hoe de stelling van Pythagoras ook werkt voor de grootte van pizza's of de tijd die nodig is om data te sorteren. Ik vond dit een tof voorbeeld:
Some programs with n inputs take n2 time to run (bubble sort, for example). In terms of processing time:
50 inputs = 40 inputs + 30 inputs
Pretty interesting. 70 elements spread among two groups can be sorted as fast as 50 items in one group. (Yeah, there may be constant overhead/start up time, just work with me here).
 Internetbureau Rotterdam
Internetbureau Rotterdam 
