Wiskundemeisjes
Archief voor categorie 'Puzzels'

Op een afgelegen eiland woont een stam van duizend mensen. Er zijn 100 mensen met blauwe ogen en 900 mensen met bruine ogen, maar dit weten de eilandbewoners zelf niet. Hun religie verbiedt de bewoners namelijk om de kleur van hun eigen ogen te weten, het is zelfs verboden om over de kleur van ogen te praten. Op het eiland is geen enkel spiegelend oppervlak te vinden, dus bewoners kunnen in principe niet ontdekken welke kleur ogen ze hebben. Als iemand tóch ontdekt welke kleur ogen hij (of zij) heeft, dan pleegt deze persoon de volgende dag om 12 uur 's middags ritueel zelfmoord op het dorpsplein - in aanwezigheid van de complete stam.
Op een dag komt er een blauwogige bezoeker op het eiland. Hij wint het vertrouwen van de stam en op een avond spreekt hij op het dorpsplein de complete stam toe. Hij weet niets van hun religie en zegt in zijn toespraak: "Wat grappig dat er op dit eiland ook mensen met blauwe ogen wonen."
Wat is het gevolg van deze uitspraak?

Natuurlijk is het erg onrealistisch dat er zo'n eiland bestaat. Maar dit is een wiskundige puzzel, dus neem even aan dat dit allemaal kan. Neem ook aan dat alle bewoners volledig logisch redeneren (als ze uit de feiten die zij kennen met een logische redenering een conclusie kunnen trekken, dan doen ze dat ook) en ook dat ze de regels van hun godsdienst volgen. En de bewoners weten van elkaar dat ze devoot zijn en ook dat de anderen allemaal volledig logisch redeneren, en ook dat weten ze van elkaar, enzovoorts. En omdat de stam zo geobsedeerd is door oogkleur, houdt iedereen precies bij hoeveel van de anderen bruine of blauwe ogen hebben.
Dus nogmaals: wat gebeurt er na deze wat ongelukkige uitspraak van de bezoeker?
Op The Prime Puzzles & Problems Connections staan (zoals de titel van de site al suggereert) een heleboel aardige puzzels met priemgetallen. Voor nieuwe lezers: een priemgetal is een getal dat precies twee delers heeft: 1 en zichzelf. Hieronder een voorbeeld van zo'n opgave.

Zoek twaalf verschillende getallen zodat je met deze getallen op twee dobbelstenen altijd een priemgetal krijgt als som van de ogen die je gooit. Je zoekt dus twee dobbelstenen met zes zijden waarbij elk van de 36 mogelijke combinaties van worpen optelt tot een priemgetal.
- Wat is de minimale oplossing?
- Wat is de minimale oplossing als de 36 mogelijke priemgetallen ook allemaal verschillend moeten zijn?
Ja ja, George heeft drie tetraëders met ribbenlengte 1 in een kubus met ribbenlengte 1 gepast! (Als je niet weet waarom dat bijzonder is, lees dan deze post even na, en vooral ook de reacties.)
Jan van de Craats mailde ons al een mooi plaatje met de gevonden oplossing:
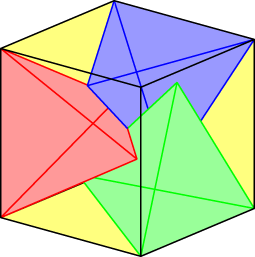
Maar de vraag blijft staan: kan iemand bewijzen dat er geen vier tetraëders met ribbe 1 in een kubus met ribbe 1 passen?
Toevoeging 14 januari: Nico Bakker stuurde ons dit filmpje, om een beter ruimtelijk idee te krijgen.
Jan van de Craats mailde ons een interessante opgave die hij heel lang geleden verzon voor de Pythagoras-olympiade.
Hoeveel tetraeders (regelmatige viervlakken) met ribbenlengte 1 passen er in een kubus met ribbenlengte 1?
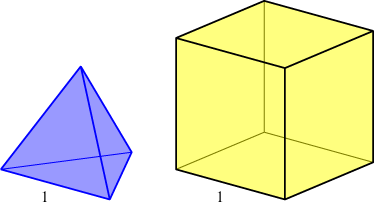
Wie weet de oplossing en vooral: wie kan bewijzen dat zijn oplossing klopt?
Jeanine schreef laatst al over Arabesk waar je onder andere mooie wiskundige houten puzzels kunt kopen. Op Pientere puzzels vind je werkbeschrijvingen om zelf zulke puzzels te maken.


Ik heb helaas twee linkerhanden, maar dit leek me een leuke tip voor mensen die wel kunnen omgaan met een figuurzaag...
Fokko van de Bult verdedigt komende donderdag in Amsterdam zijn proefschrift Hyperbolic Hypergeometric Functions. Stelling 8 van dat proefschrift lijkt verdacht veel op een leuke wiskundepuzzel.

Stel dat de schaakkwaliteiten van een groep van n mensen volledig geordend zijn, in de zin dat als speler A beter is dan B hij altijd van B wint, en als B altijd van C wint, wint ook A altijd van C. Stel bovendien dat elke speler na 10 verloren wedstijden verloren te hebben (onafhankelijk van het aantal gewonnen wedstrijden) teleurgesteld naar huis gaat. Dan bestaat er een algoritme om indelingen te maken, alleen gebaseerd op uitkomsten van voorgaande wedstrijden, zodat met zekerheid de complete ordening in sterkte van deze groep spelers te bepalen is dan en slechts dan als n < 210.

Heeft een van jullie een idee hoe het algoritme de indelingen bepaalt?
Fokko waarschuwde ons dat dit niet echt een makkelijk probleem is. Het zou qua niveau een opgave op de Internationale Wiskunde Olympiade kunnen zijn. Fokko won zelf twee zilveren medailles op de internationale olympiade in 1997 en 1998 en traint al jaren de Nederlandse deelnemers.
In wiskundetijdschrift Pythagoras staat elk jaar een prijsvraag. Zo ook nu! De puzzel van dit jaar is gebaseerd op tangram. Matthijs Coster (bekend van de befaamde coster-getallenprijsvraag van vorig jaar, waar we hier en hier over schreven) bedacht een variant: pygram. Je hebt nog de hele kerstvakantie de tijd om aan de prijsvraag te werken, want inzendingen moeten vóór 8 januari binnen zijn.
De pygram-stukjes zien er zo uit:

Kortom: ga aan de slag, ga knippen en plakken of figuurzagen, leef je uit met verf! Verzin zoveel mogelijk convexe figuren, of maak figuren met een zo groot of zo klein mogelijke omtrek.
Met de Pygramprijsvraag kun je op diverse manieren prijzen verdienen. Er zijn vier opdrachten in de categorie 'wiskundig' en twee in de categorie 'artistiek'. De precieze opdrachten staan hier in een printversie.
Iedereen kan aan de Pygramprijsvraag meedoen: leerlingen, beroepswiskundigen, hobbyïsten, enzovoorts. Ook als klas kun je inzenden. Opdracht A1 is bij uitstek geschikt voor een klasseninzending. In elke categorie is er een hoofdprijs van 100 euro. De jury behoudt zich het recht voor om niet in elke categorie de hoofdprijs uit te reiken, of om de prijs te verdelen over meer dan één inzender.

Fred mailde ons over Arabesk, een mooie webwinkel vol leuke spulletjes. Arabesk verkoopt artikelen die gemaakt zijn door kunstenaars of ontwerpers die zich hebben laten inspireren door wiskunde, natuurkunde en logica.

Als je even op de site van Arabesk snuffelt ontdek je een boel leuks. Puzzels van hout en touw (die ik zelf vaak heel leuk vind, maar wel moeilijk), speelgoed, spelletjes en allerlei mooie objecten.

En er is goed nieuws: Arabesk heeft nu ook een echte winkel! Contactinformatie:
Oostzeedijk Beneden 111-115, 3061 VP Rotterdam
Openingstijden (voorlopig onder voorbehoud): dinsdag t/m zaterdag, 11.00 tot 18.00 uur
U kunt ook een afspraak maken: 010 2140361 of per e-mail.
Peter Winkler maakte een lijst met puzzels waarvan je denkt dat je ze niet goed gehoord hebt. Ze lijken te moeilijk of juist te makkelijk om op te lossen. Veelgehoorde reacties op deze puzzels zijn "Klopt dit wel echt?" en "Wacht, volgens mij heb ik het verkeerd verstaan". Hierbij mijn favoriete puzzel uit deze lijst, misschien volgen er later meer.

In een ver land staat een gevangenis met een wiskundig onderlegde directeur. Hij biedt honderd gevangen een kans om vrij te komen. Hij zet een rij van honderd houten kistjes in een kamer. Hij stopt in elk kistje de naam van één van de gevangenen, elke naam komt precies één keer voor. De gevangenen worden één voor één naar deze kamer gebracht. Elke gevangene mag maximaal vijftig kistjes openmaken en kijken welke naam erin zit. Hij moet de kamer daarna precies zo achterlaten als hij binnenkwam en hij mag niet meer met de andere gevangenen praten.
De gevangenen mogen vooraf een strategie verzinnen en die zullen ze hard nodig hebben. Want ze worden alleen vrijgelaten als elke gevangene de kist met zijn eigen naam erin openmaakt. Als dat níet lukt, dan worden ze allemaal onthoofd. Er is een strategie, waarbij de gevangenen meer dan 30% kans hebben om vrij te komen. Wat is deze strategie?
Merk op dat als elke gevangene vijftig willekeurige dozen openmaakt, de kans dat ze vrij komen gelijk is aan (1/2)100 en dat is heel wat kleiner dan 30%.
p.s. Je hebt het echt goed gelezen: meer dan 30%!
Camiel stuurde ons een grappige logica-puzzel, gemaakt door Shaun Spalding. Het is een parodie op de Amerikaanse Law School Admission Test (LSAT voor vrienden).
LSAT PRACTICE.
A concerned father drops three boys (Peter, Dom, and Björn), three girls (Henrietta, Elaine, and Meghan), and his daughter (Lorelei) off at the local mall’s theater. He wants to know which one of the boys will be making out with his daughter during the movie. He knows that each of the eighth-graders will make out at least once but not more than twice before the movie ends. He also knows that the following conditions must apply:
Elaine will not make out with Björn until she’s made out with Peter (because she and Björn are in an open relationship and she’s testing the waters).
Henrietta will not make out with Peter or Dom (because she only dates older guys).
If Lorelei makes out with both Henrietta and Elaine, then Peter and Björn will make out. (They made a bet.)
Meghan will always make out last (because she’s ugly).
Dom will always be paired with Meghan (because he’s desperate).

1. If Lorelei goes to get popcorn and is forced to sit between Dom and Meghan during the previews, which of the following must be true?
(a) Peter makes out with Elaine.
(b) Björn makes out with Elaine.
(c) Henrietta talks to Dom awkwardly about world-geography class to avoid his advances.
(d) Lorelei is unable to take the sexual tension between Dom and Meghan and pretends she needs to go to the bathroom so she can switch seats.
(e) Lorelei’s father is worried his daughter is growing up too fast.
De vier andere vragen (en antwoorden) zijn te vinden bij McSweeney’s.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
