Wiskundemeisjes
Vorige week vroeg ik jullie: wat is de mooiste rechthoek?

Op het moment dat ik dit schrijf, hebben er 485 mensen gestemd en is dit de top 3:
- Rechthoek 8 (met 94 stemmen)
- Rechthoek 11 (met 72 stemmen)
- Rechthoek 10 (met 68 stemmen) .
Het plaatje en het idee kwamen van MathTrek. In hun artikel staat dat rechthoek 11 verhoudingen heeft die het dichtste bij de gulden snede liggen. Als eigenwijze wiskundige heb ik het plaatje vergroot, geprint en opgemeten met mijn geodriehoek. Misschien komt het doordat ik de zwarte lijntjes meeneem, maar ik kom op een andere guldenste rechthoek.
De gulden snede is gelijk aan (√5+1) /2, wat ongeveer 1,62 is. Dit is mijn gemeten top drie van meest gulden rechthoeken.
- Rechthoek 1 met verhouding 1,62
- Rechthoek 11 met verhouding 1,58
- Recthoek 3 met verhouding 1,67.
De grote favoriet rechthoek 8 heeft als verhouding 1,71 en rechthoek 10 zit helemaal ver van de gulden snede af met een verhouding van 1,86.
Wat kunnen we nu concluderen? Eigenlijk nogal weinig. De verschillen in de verhoudingen zijn erg klein en meetfouten spelen ongetwijfeld ook nog een rol. Uit de literatuur over de gulden snede hypothese (het vermoeden dat mensen de gulden snede als mooiste kiezen) begreep ik, dat de resultaten van dit soort onderzoek sterk afhangen van de uitvoering van het onderzoek.
Ik vind het wel grappig dat rechthoek 4 zo impopulair is, terwijl zijn verhouding (1,91) dichtbij die van rechthoek 10 ligt. Blijkbaar vinden we liggende rechthoeken mooier...
Een bekend verschijnsel voor iedereen die wel eens opgaven nakijkt: het antwoord is juist, maar de afleiding klopt helemaal niet. Helaas is de onderstaande afleiding geen grap, maar een serieuze uitwerking van een student.

Hoeveel fouten zien jullie? Op Common Errors in College Math staat een uitgebreide verzameling van veel gemaakte fouten.
Eerder dit jaar studeerde Aldine Aaten af in de wiskunde in Leiden. Haar afstudeerrichting is communicatie en educatie. Ze schreef een erg interessante scriptie over de vraag hoe wiskundestudenten hun vak en hun studie ervaren: Ik begreep er niets van - het leek wel algebra. Daar was nog maar weinig onderzoek naar gedaan. Aldine interviewde wiskundestudenten uit Leiden en ze heeft vragenlijsten gemaakt die zijn ingevuld door wiskundestudenten van de Universiteit Leiden, de TU Delft en de UvA.
Ze koos dit onderwerp op grond van haar eigen ervaringen als wiskundestudent. De buitenwereld denkt meestal: "Wat knap, dat jij wiskunde kan!" Maar wat "wiskunde kunnen" betekent, is niet zo duidelijk. Betekent dat dat alle wiskundestudenten zonder problemen hun studie doorlopen? Nee. Betekent het dat wiskundestudenten wiskunde nooit moeilijk vinden? Ook niet. Zoals een van de geïnterviewde studenten opmerkt: je kan wiskunde zo moeilijk maken als je wil. En veel studenten blijken juist de uitdaging te waarderen. Wiskundestudenten gaan wel op een constructieve manier om met de negatieve gevoelens die ze ervaren tijdens het doen van wiskunde.

Aldine heeft onderzocht hoe wiskundestudenten omgaan met de stof, maar ook hoe ze omgaan met tegenslagen in hun studie, zoals de stof niet begrijpen of een onvoldoende halen. Er is onderscheid gemaakt tussen de volgende groepen: man/vrouw, bachelor-/masterstudenten en studenten die van zichzelf zeggen dat ze ondergemiddeld, gemiddeld of bovengemiddeld goed zijn in wiskunde.
Op het wiskundetoernooi in september werden de wiskundemeisjes streng maar rechtvaardig gejureerd door Mai Gehrke. Wij grepen de gelegenheid aan om haar te vragen wie haar favoriete (nog levende!) wiskundige is.
Mai Gehrke
Gehrke is sinds mei dit jaar hoogleraar algebra in Nijmegen. Ze studeerde en promoveerde aan de University of Houston.

Ze werkt aan topologische methoden in algebra en algebraïsche logica. Ze mailde ons meer uitleg:
"One wants to understand a logic from two points of view: semantically and syntactically. The syntax is used for describing the logic. In computer science this is important for specification and verification of systems. Semantics identify the meaning of the logic. In computer science this describes the phase-space of the system: its possible states and what transitions are possible when running the system. This point of view carries the intuitions and, technically, this is often the side on which it is easiest to solve problems effectively. Accordingly it is of great interest to have both views available. With topological duality you can move from semantics to syntax and vice versa."
Bjarni Jónsson
Toen Gehrke begon als wiskundige, was ze een groot fan van Marshall Stone (van bijvoorbeeld de Stone–Čech compactification), maar hij is in 1989 overleden. Later ontmoette ze Bjarni Jónsson en kreeg ze de kans om met hem samen te werken. Hij is nu zeker haar keuze als favoriete wiskundige. Leuk detail: op het moment dat dit artikel verschijnt, is ze op bezoek bij hem!

De IJslandse Jónsson promoveerde aan Berkeley en werkte lange tijd aan de Vanderbilt University. Hij is inmiddels met emiritaat. Zijn vakgebied is de theorie van roosters en universele algebra's. Die tak van wiskunde ontstond in de 20ste eeuw. Gehrke: "Jónsson is echt de grootvader van dit vakgebied, een groot deel van alle resultaten komt van hem. Hij heeft resultaten met vertakkingen in zoveel richtingen (groepentheorie, logica) dat het moeilijk is om te zeggen wat zijn beroemdste resultaat is." Ook hier mailde Mai Gehrke ons na het interview nog meer uitleg:
"In universal algebra he is the one who realized that congruence distributivity is a really powerful notion (an algebra is congruence distributive if the lattice of all its quotients is distributive). A particular result is Jónsson's lemma which states that if you have a class K of congruence distributive algebras, then you only have to look among the homomorphic images of subalgebras of ultraproducts of elements K when looking for the basic building blocks of the equational class of algebras generated by K."
Ook zijn werk (met Tarski) aan Booleaanse algebra's met operatoren is erg beroemd en erg belangrijk voor het werk van Gehrke in algebraïsche logica en dualiteitstheorie.
Gehrke: "Jónsson is misschien geen charismatisch leiderstype, maar de sterkte en de schoonheid van zijn ideeën hebben velen - waaronder mij- geïnspireerd. Hij is erg scherp, denkt ontzettend snel en heeft een ongelooflijk gevoel voor humor. Hij blaast je soms echt omver met zijn ideeën. Het was fantastisch om met hem te werken."
Gehrkes samenwerking met Jónnson was op zijn zachtst gezegd opmerkelijk. "We werkten aan dezelfde universiteit, maar zagen elkaar niet. Hij legde een keer wat aantekeningen in mijn postvakje en ik ging daarmee verder aan het werk. Ik stopte mijn resultaten in zijn postvakje. Later vond ik zijn antwoord weer in mijn postvakje, zo ging het vijf maanden door. Ik heb nooit zo hecht met iemand anders samengewerkt, alle resultaten waren van echt van ons samen. En het waren grote resultaten. Op een gegeven moment kwam ik hem tegen in de gang. Ik stelde voor om eens over ons werk te praten. Hij antwoordde dat hij eigenlijk liever niet praatte over lopend onderzoek, omdat hij dan te enthousiast werd en te snel conclusies trok. Ik vond dat verbazingwekkend voorzichtig van de grootste autoriteit op dit gebied."
Jónnson is inmiddels achtentachtig, maar werkt nog altijd hard. Een tijd terug werd Gehrke gebeld door de vrouw van Jónnson om te zeggen dat hij niet kon schrijven. Hij kreeg namelijk een vijfvoudige bypass. Een dag later (!) schreef hij zelf een brief vanuit het ziekenhuis. Dat bewijs was het enige onjuiste dat hij ooit naar Gehrke stuurde.
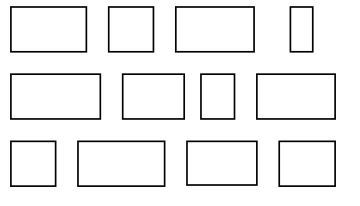
Wat vinden jullie de mooiste rechthoek? Voor het gemak heb ik de rechthoeken hieronder genummerd.

[poll=6]
Zoals jullie misschien al raadden: één van deze rechthoeken heeft verhoudingen die dicht bij de gulden snede liggen. Ik vroeg me af of mensen die nou echt mooier vinden. Later deze week zal ik vertellen welke de gulden rechthoek is!
Daniel Tammet is een 28-jarige man uit Engeland die heel bijzonder is: hij heeft een aantal zeldzame aandoeningen tegelijk. Hij heeft het Asperger-syndroom, hij is een savant en hij heeft synesthesie. Hij schreef een boek over zijn leven: Born on a blue day, nu in het Nederlands vertaald als Op een blauwe dag geboren.

Het Asperger-syndroom is een vorm van autisme, wat betekent dat hij grote moeite heeft met sociale interactie en dat hij rigide en stereotype gedragspatronen vertoont. Tammet heeft een extreme behoefte aan orde en regelmaat: hij eet elke ochtend precies 45 gram pap als ontbijt en hij moet altijd weten hoeveel kledingstukken hij aan heeft. Het Asperger-syndroom onderscheidt zich van andere vormen van autisme doordat mensen die Asperger hebben geen taalachterstand of problemen met congnitieve ontwikkeling vertonen.
Een savant is iemand die op een heel specifiek gebied extreem uitzonderlijke prestaties levert. Tammet kan bijvoorbeeld extreem goed rekenen en getallen onthouden. Ook kan hij heel snel talen leren: hij leerde het IJslands, dat als een moeilijke taal bekend staat, binnen een week zó goed dat hij zich staande kon houden in een IJslands tv-interview. De meeste savants hebben echter een ontwikkelings- of mentale handicap, waardoor hun IQ lager dan gemiddeld is. Bij Tammet is dat niet het geval. Wat zo bijzonder aan hem is, is dat hij zelf kan uitleggen wat er in zijn hoofd gebeurt als hij rekent of een getal onthoudt.
Maarten vroeg ons of we Echochrome, het Escher-achtige computerspel al hadden gezien. Nee dus! Sony is bezig met dit spel voor de PlayStation® Portable (PSP voor vrienden). De eerste beelden zijn zeker intrigerend. Het lijkt meer op een mooie puzzel dan op een spelletje.
Het spel is voorlopig niet te koop, de release wordt in maart 2008 verwacht. Kunnen we in de tussentijd vast sparen voor een PSP.
We schreven eerder al over een heldhaftige tatoeage van de gulden snede. Bart tipte ons dat op Flickr een groep Science Tattoos is te vinden. Hierbij wat wiskundige voorbeelden!








Vanaf nu kun je een wiskundewandeling maken door Utrecht! Zo'n wandeling bestond al in Amsterdam. Aan wat je ziet worden wiskundige vragen gekoppeld, die niet veel voorkennis vereisen: twee of drie jaar voortgezet onderwijs is genoeg.

Duur wandeling: 1,5 uur • 21 vragen; tips; ruimte voor antwoorden • 20 pagina’s A5; 120 grams papier • Veelkleurendruk met foto’s • Antwoorden staan op internet • Uitsluitend per mail te bestellen: wisc@planet.nl • EUR 5 per boekje (kostprijs); minimale afname: twee exemplaren.
Wie weet zie je de wiskundemeisjes binnenkort door Utrecht slenteren!
Peter Winkler maakte een lijst met puzzels waarvan je denkt dat je ze niet goed gehoord hebt. Ze lijken te moeilijk of juist te makkelijk om op te lossen. Veelgehoorde reacties op deze puzzels zijn "Klopt dit wel echt?" en "Wacht, volgens mij heb ik het verkeerd verstaan". Hierbij mijn favoriete puzzel uit deze lijst, misschien volgen er later meer.

In een ver land staat een gevangenis met een wiskundig onderlegde directeur. Hij biedt honderd gevangen een kans om vrij te komen. Hij zet een rij van honderd houten kistjes in een kamer. Hij stopt in elk kistje de naam van één van de gevangenen, elke naam komt precies één keer voor. De gevangenen worden één voor één naar deze kamer gebracht. Elke gevangene mag maximaal vijftig kistjes openmaken en kijken welke naam erin zit. Hij moet de kamer daarna precies zo achterlaten als hij binnenkwam en hij mag niet meer met de andere gevangenen praten.
De gevangenen mogen vooraf een strategie verzinnen en die zullen ze hard nodig hebben. Want ze worden alleen vrijgelaten als elke gevangene de kist met zijn eigen naam erin openmaakt. Als dat níet lukt, dan worden ze allemaal onthoofd. Er is een strategie, waarbij de gevangenen meer dan 30% kans hebben om vrij te komen. Wat is deze strategie?
Merk op dat als elke gevangene vijftig willekeurige dozen openmaakt, de kans dat ze vrij komen gelijk is aan (1/2)100 en dat is heel wat kleiner dan 30%.
p.s. Je hebt het echt goed gelezen: meer dan 30%!
 Internetbureau Rotterdam
Internetbureau Rotterdam 
