Wiskundemeisjes

Na het bewijzen van het vermoeden van Poincaré en het weigeren van de Fields-medaille gaat Grigori Perelman op zoek naar een nieuwe baan...

Om alles te begrijpen is het artikel Manifold Destiny van Sylvia Nasar en David Gruber een aanrader. Bijvoorbeeld:

When a member of a hiring committee at Stanford asked him for a C.V. to include with requests for letters of recommendation, Perelman balked. “If they know my work, they don’t need my C.V.,” he said. “If they need my C.V., they don’t know my work.”

Er is ook een deel twee: A Dutiful Mind (!).

Op deel 3 tot en met n moeten we helaas nog even wachten aldus de makers.

The production of the next video is facing serious challenges, as Dr. Perelman is in hiding and his activities are unknown. Our investigative team is still on the job, however, and we will share whatever news they find as they find it.

Een goede reden om aanstaande zondag vroeg op te staan: Robbert Dijkgraaf geeft een kinderlezing in Nemo! Om 11 uur begint de lezing Tot hoeveel kun je tellen?

Een voetbalelftal bestaat uit 11 spelers en in Artis vind je ruim 6100 dieren. Dat is nog te begrijpen en te tellen. Maar hoeveel 6 miljard aardbewoners zijn of dat er 200.000.000.000 sterren in ons melkwegstelsel staan, daar kunnen maar weinig mensen zich iets bij voorstellen. Wiskundige prof. dr. Robbert Dijkgraaf van de Universiteit van Amsterdam weet alles over oneindig tellen.

Deze lezing gaat over hele grote getallen, zo groot dat de meeste mensen zich er niets bij kunnen voorstellen. Dijkgraaf onderzoekt samen met de kinderen of er een punt bestaat dat je niet meer verder kunt tellen. Ze gaan op zoek naar de betekenis van grote getallen en het begrip oneindigheid.

Een echte aanrader, want Dijkgraaf is erg enthousiast en een goede spreker, zeker ook voor kinderen! Alle informatie kun je vinden op deze site.

Dit weekend zijn mijn vriend en ik verhuisd (en Jeanine verhuist komend weekend, dus het zijn drukke tijden voor de wiskundemeisjes). We wilden in onze nieuwe woonkamer een mooi wiskundig patroon leggen met tapijttegels. Uiteindelijk hebben we een Sierpinski tapijt gelegd. Ik ben zo trots op het resultaat dat ik het aan jullie wil laten zien.

Zoals de kenners gelijk zullen zien is dit slechts de tweede iteratie van het Sierpinski tapijt. Na een boel iteraties krijg je een mooie fractal:

Jammer genoeg is onze woonkamer te klein voor meer iteraties en waren er geen vrijwilligers om de tapijttegels in kleinere vierkanten te snijden...

We worden vaak gevraagd wie onze lezers nu precies zijn. Dat weten we zelf ook niet, dus daarom bij deze een kleine enquête. Je kunt maximaal drie antwoorden kiezen. Doe ons een plezier en vertel ons wat je doet!

[poll=7]

Op 1 en 2 februari vinden de Nationale Wiskunde Dagen weer plaats! Wiskundedocenten uit heel Nederland verzamelen zich twee dagen lang in Noordwijkerhout voor interessante workshops, leuke lezingen, fascinerende stands en, niet te vergeten, om bij te kletsen en ideeën uit te wisselen met de rest van wiskundig Nederland.

Je snapt dat de wiskundemeisjes dit niet willen missen! We zullen dan ook de hele tijd aanwezig zijn, en we geven zelfs een lezing: De geheime bronnen van de wiskundemeisjes.

Helaas zijn de Wiskunde Dagen zo populair dat ze al zijn volgeboekt. Maar gelukkig gaat dit jaar een geheel nieuw initiatief van start op de zaterdagmiddag van de Wiskunde Dagen: Café Möbius! Geschikt voor iedereen, ook voor middelbare scholieren.

Wat is wiskunde en wat kun je ermee? In Café Möbius kan iedereen kennis maken met wiskunde en de alledaagse relevantie ervan. Beleef de intrigererende aspecten van wiskunde en zie hoe wiskunde onmisbaar is in ons dagelijkse leven. Café Möbius is alleen geopend op zaterdag 2 februari van 14 tot 18 uur. De vorm van deze middag is informeel: laagdrempelige workshops met 'open deuren' en een enkele lezing. Kortom: iedereen is welkom en de inschrijving is gratis!

Ook in Café Möbius geven de wiskundemeisjes acte de présence. We hopen veel van onze lezers daar te zien, schrijf je dus snel in!

Ja ja, George heeft drie tetraëders met ribbenlengte 1 in een kubus met ribbenlengte 1 gepast! (Als je niet weet waarom dat bijzonder is, lees dan deze post even na, en vooral ook de reacties.)

Jan van de Craats mailde ons al een mooi plaatje met de gevonden oplossing:

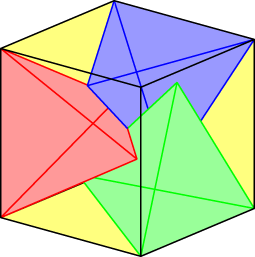
Maar de vraag blijft staan: kan iemand bewijzen dat er geen vier tetraëders met ribbe 1 in een kubus met ribbe 1 passen?

Toevoeging 14 januari: Nico Bakker stuurde ons dit filmpje, om een beter ruimtelijk idee te krijgen.

Dolf tipte ons over Random.org waar je sinds 1998 terecht kunt voor al je willekeurige getallen. Handig! Hierbij een reeks echt random getallen:

49 32 28 6 84 79 44 42 25 51 89 10 33 58 53 78 16 99 64 1 91 5 38 81 98 57 45 31 82 96 95 36 20.

Lees op de site vooral hoe ze de random getallen maken uit achtergrondruis en waarom het moeilijk is om met een computer echt willekeurige getallen te maken. Ik herhaal nog een keer deze leuke grap van Dilbert...

In het kerstnummer van NewScientist stond een leuk artikel over het spel Steen, papier, schaar. Je speelt met zijn tweeën: je telt af en dan maak je allebei tegelijk met je hand een steen (vuist), papier (vlakke hand) of schaar. Ik leerde vroeger op het schoolplein dat papier wint van steen, omdat je een steen in papier kan pakken. Steen wint van schaar, omdat je met een steen een schaar kan slijpen. En schaar wint natuurlijk van papier.

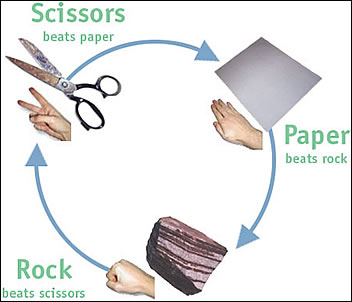
Je kunt het spel online spelen. Er blijken allerlei strategieën te bestaan en er is zelfs een heuse World RPS Society (professionals noemen het spel RPS of RoShamBo). Voor wie meer van programmeren dan van besliskunde houdt: er worden ook wedstrijden voor computerprogramma's gehouden. Al lijkt de laatste wedstrijd in 2001 te zijn gehouden...

Het artikel uit NewScientist is niet gratis toegankelijk, maar bij mental_floss vond ik online het soortgelijke How to Win at Rock-Paper-Scissors (and also how to cheat).

Jan van de Craats mailde ons een interessante opgave die hij heel lang geleden verzon voor de Pythagoras-olympiade.

Hoeveel tetraeders (regelmatige viervlakken) met ribbenlengte 1 passen er in een kubus met ribbenlengte 1?

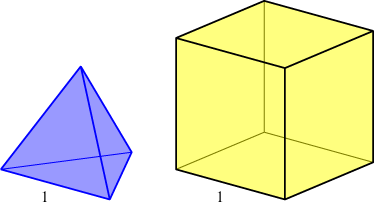
Wie weet de oplossing en vooral: wie kan bewijzen dat zijn oplossing klopt?

Het doel van de conferentie Technology, Entertainment, Design (TED voor vrienden) is het verspreiden van ideeën. Het is ontzettend moeilijk en duur om zo'n conferentie bij te wonen, maar dit is 2008, dus een deel van de presentaties staat online. Sprekers krijgen 18 minuten om de presentatie van hun leven te geven. Sommige voordachten zijn zo goed, dat je als kijker in die korte tijd heel veel leert. Tussen de sprekers zitten grote namen als Richard Dawkins, Bill Clinton en Larry Page. Er staan twee wiskundige voordrachten online: Arthur Benjamin met "Mathemagic" en Ron Eglash over African fractals.